確率的ソロー・モデル#
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import japanize_matplotlib
import py4macro
# numpy v1の表示を使用
np.set_printoptions(legacy='1.21')
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
はじめに#
景気循環を理解する上で全要素生産性の役割が強調される研究があるが,その導入として全要素生産性の特徴について検討する。またソロー・モデルを使い,全要素生産性が確率的に変動する簡単な景気循環モデルのシミュレーションを通してマクロ変数の特徴を考察する。
景気循環の要素分解#
説明#
マクロ変数の特徴を捉えるにはホワイト・ノイズよりもAR(1)の方がより適している。では,どの様な形でAR(1)をマクロ・モデルに導入すれば良いのだろうか。現在盛んに行われている景気循環研究はDSGEモデル(Dynamic Stochastic General Equilibrium Model)と呼ばれるモデルに基づいており、DSGEは名前が示すように次のような特徴がある。
時間軸に沿ってマクロ変数の変化を考察する動学的な特徴
確率的な要因の重要な役割
合理的期待に基づく将来を見据えた消費者と企業の最適行動
一般均衡のモデル
そして,DSGE研究の先駆けとなったモデルが実物的景気循環モデル(Real Business Cycles Model; RBCモデル)と呼ばれる理論である。詳細については後の章に譲るが,基本的なアイデアは簡単で全要素生産性(TFP)がAR(1)に従って確率的に変動し,それが消費者と企業の経済行動に影響することにより景気循環が発生するという理論である。ここではデータを使い全要素生産性の性質を考察する。RBCモデルで需要な役割を果たす労働時間についてもデータを使い特徴を探ることにする。
データ#
次の生産関数を仮定する。
\(Y_t\):GDP
\(K_t\):資本ストック
\(H_t\):総労働時間(労働者数\(\times\)労働者平均労働時間)
\(A_t\):TFP
TFPについて解くと次式を得る。
景気循環を考えているため、TFPを計算する際には次の点を考慮することが望ましい。
年次データではなく四半期データを使う(年次データでは短期的な変動を捉えることができない)。
\(H_t\)は労働者数ではなく,総労働時間とする(短期的な労働供給の変化を捉えるため)。
\(K_t\)は資本ストックの稼働率を考慮したデータとする(短期的に実際に生産に使われた資本ストックの変化を捉えるため)。
ここでは1と2のみを考慮したデータを使いTFPの変動を考えることにする。これにより資本ストックの稼働率はTFPの一部となってしまうが,RBCモデルの基本的なアイデアは変わらない。
データを読み込もう。
df = py4macro.data('jpn-q')
ここで読み込んだデータdfには次の変数が含まれている(詳細はGDP:水準・トレンド・変動を参照)。
期間:1980年Q1〜
gdp:国内総生産(支出側)capital:資本ストックemployed:就業者hours:労働者1人あたり月平均就業時間(以下では「平均労働時間」と呼ぶ)total_hours:総労働時間(hours\(\times\)employed)
まずgdpのトレンドからの乖離(%)をgdp_cycleとして作成しておく。
df['gdp_trend_log'] = py4macro.trend( np.log(df['gdp']) )
df['gdp_cycle'] = 100 * ( np.log( df['gdp'] ) - df['gdp_trend_log'] )
労働時間と雇用の特徴#
平均労働時間hours,就業者数employed,総労働時間total_hoursの特徴を考えてみる。まずサイクルを計算するが、次の点に留意し計算方法が異なる。
hoursは上限があり、長期間持続的に上昇もしくは減少しない。employedは長期間持続的に上昇もしくは減少することは可能な変数。total_hoursは、hoursとemployedの掛け算となっているため、長期間持続的に上昇もしくは減少することは可能な変数。
df['hours_trend'] = py4macro.trend(df['hours'])
df['hours_cycle'] = 100 * np.log( df['hours']/df['hours_trend'] )
df['employed_trend_log'] = py4macro.trend( np.log(df['employed']) )
df['employed_cycle'] = 100 * ( np.log( df['employed'] ) - df['employed_trend_log'] )
df['total_hours_trend_log'] = py4macro.trend( np.log(df['total_hours']) )
df['total_hours_cycle'] = 100 * ( np.log( df['total_hours'] ) - df['total_hours_trend_log'] )
最初に,平均労働時間を考えよう。
df.plot(y=['hours','hours_trend'])
pass
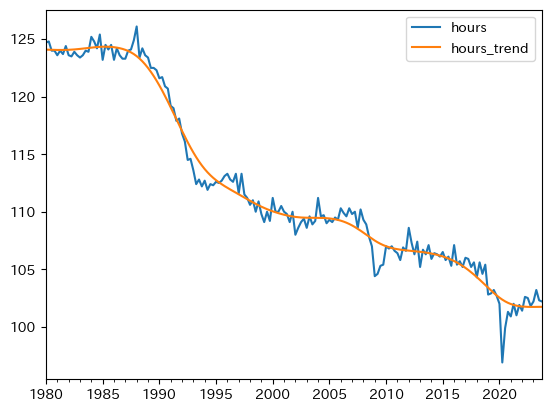
平均労働時間は長期的に減少傾向にある。2020年の平均が100に標準化しているので,1980年代には約25%長かったことを示している。次に,就業者数を図示する。
ax_ = df.plot(y='employed')
np.exp( df['employed_trend_log'] ).plot(ax=ax_)
pass
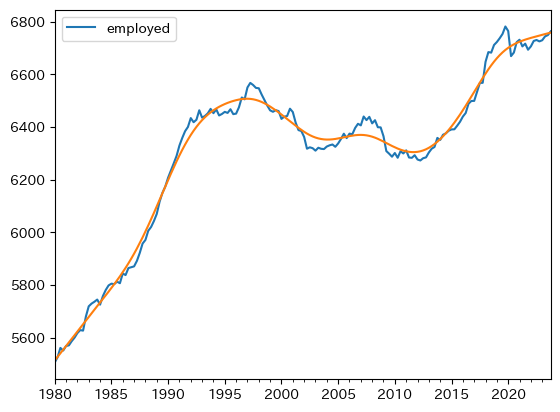
コードの説明
df['employed_trend_log']は、トレンドを対数化した値となる。指数化し元の数値に戻すためにnp.exp()を使っている。また、np.exp(df['employed_trend'])はSeriesを返すことになり、そのメソッドplot()を使って図示している。
一方,雇用者数は増加傾向にある。女性の労働市場参加率の増加や,雇用形態の変化(非正規など)の影響と考えられる。
上の2つの変化を反映したのが総労働時間の変化である。
ax_ = df.plot(y='total_hours')
np.exp( df['total_hours_trend_log'] ).plot(ax=ax_)
pass
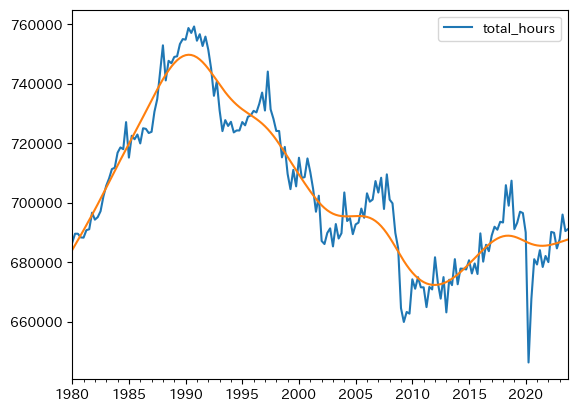
バブル崩壊後は減少傾向にあるが,過去10年間に持ち直して来ている。これは雇用の拡大の要因が大きい。
雇用と労働時間の変動(トレンドからの乖離率)を比べてみよう。
ax_ = df.plot(y=['hours_cycle','employed_cycle'])
ax_.axhline(0, c='red', lw=0.5)
pass
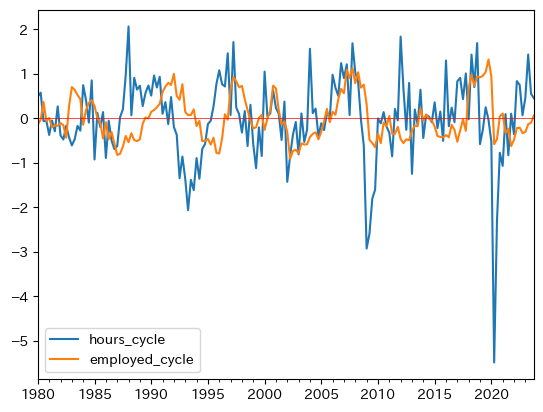
次の2つの点を指摘できる。
労働時間の方が変動が大きい。即ち,総労働時間の調整は就業者数よりも労働時間を通して行われていることが伺える。
就業者数の変化は、労働時間の変化を後追いする傾向がある。これは就業者の調整費用がより高いためであろう。
自己相関係数を計算してみる。
cycle_list = ['hours_cycle','employed_cycle','total_hours_cycle']
var_list = ['平均労働時間','就業者数','総労働時間']
print(' 自己相関係数\n----------------------')
for c, v in zip(cycle_list,var_list):
ac = df[c].autocorr()
print(f'{v:<5}\t{ac:.3f}') # 1
自己相関係数
----------------------
平均労働時間 0.486
就業者数 0.830
総労働時間 0.580
コードの説明
:<5はf-stringで代入する変数vのスペースを5に設定し左寄せ<にすることを指定している。また:.3fは小数点第三位までの表示を指定している。
就業者数がより大きな自己相関係数の値となっており,就業者での調整により時間がかかるためである。即ち,今期の就業者数は前期の就業者数に依存するところが大きいという意味である。
次に,GDPのトレンドからの乖離との相関係数を計算してみる。
print('GDPサイクルとの相関係数')
print('-------------------------')
for c, v in zip(cycle_list,var_list):
corr = df[['gdp_cycle',c]].corr().iloc[0,1]
print(f'{v:<9}\t{corr:.3f}')
GDPサイクルとの相関係数
-------------------------
平均労働時間 0.747
就業者数 0.451
総労働時間 0.820
やはり非常に強い正の相関があり,平均労働時間の影響が強いようである。
df[['gdp_cycle', 'total_hours_cycle']].plot()
<Axes: >
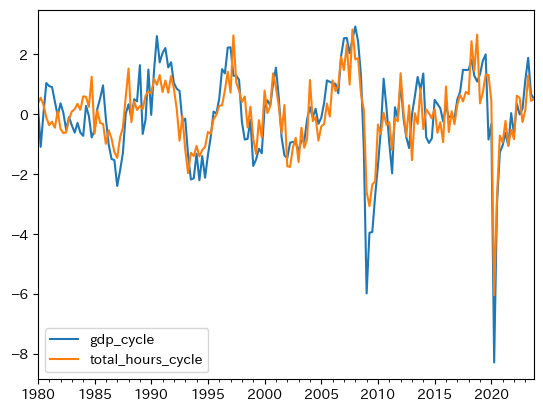
資本ストックの特徴#
df['capital_trend'] = py4macro.trend( np.log(df['capital']) )
df['capital_cycle'] = 100 * (
np.log( df['capital']) - df['capital_trend']
)
ax = np.log(df['capital']).plot()
df['capital_trend'].plot(ax=ax)
# df['capital_cycle'].plot()
<Axes: >
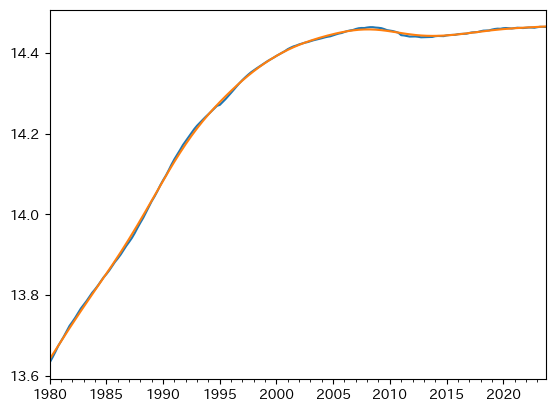
df['capital_cycle'].autocorr()
0.9510630841084321
df[['gdp_cycle', 'capital_cycle']].corr().iloc[0,1]
0.146128728047154
df[['gdp_cycle', 'capital_cycle']].plot()
<Axes: >
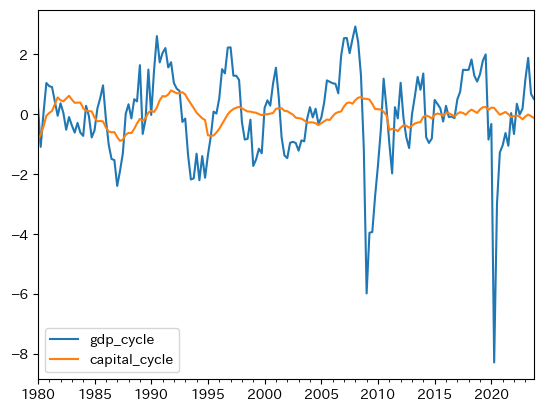
TFPの特徴#
TFPの水準,トレンド,変動(サイクル)を計算するが,資本の所得分配率を次のように仮定する。
a = 0.36
# 全要素生産性(対数)の計算
df['tfp_log'] = np.log( df['gdp']/( df['capital']**a * df['total_hours']**(1-a) ) )
# 全要素生産性のトレンド(対数)の計算
df['tfp_log_trend'] = py4macro.trend( df['tfp_log'] )
# 全要素生産性のトレンドからの乖離率の計算
df['tfp_cycle'] = 100 * ( df['tfp_log'] - df['tfp_log_trend'] )
# 全要素生産性とトレンドのプロット
ax = df.plot(y=['tfp_log','tfp_log_trend'])
ax.set_title('全要素生産性とトレンド(対数)', size=20)
pass
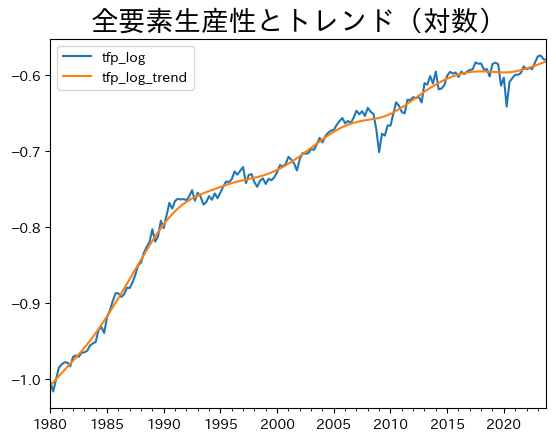
全要素生産性の変動をプロットしよう。
ax = df.plot(y='tfp_cycle')
ax.axhline(0, c='red')
ax.set_title('全要素生産性の変動(%)', size=20)
pass
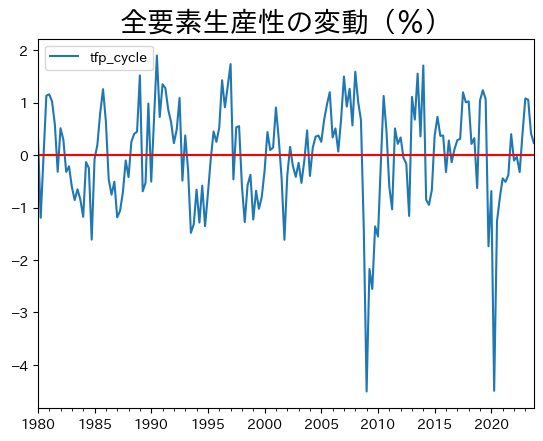
この図から全要素生産性の変動は大きいことが分かる。変動の最小値と最大値を確認してみよう。
df['tfp_cycle'].min(), df['tfp_cycle'].max()
(-4.507030513477894, 1.8997202364909982)
正の乖離は2%近くあり,負の乖離は4%以上となる。リーマンショック時を除くと正も負も絶対値で概ね2%以内に収まっている。
GDPと一緒にプロットしてみよう。
df[['gdp_cycle','tfp_cycle']].max()
gdp_cycle 2.934479
tfp_cycle 1.899720
dtype: float64
ax_ = df.plot(y=['gdp_cycle','tfp_cycle'])
ax_.set_title('GDPとTFPの変動(%)',size=20)
pass
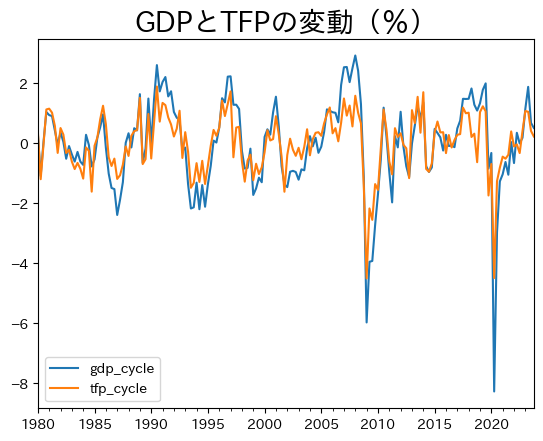
同じ方向に動いているのが確認できる。GDPの変動との相関係数を計算してみると,非常に高いことがわかる。
df[['gdp_cycle','tfp_cycle']].corr().iloc[0,1]
0.9011737000765306
以前の計算結果を使うと,この数字はGDPのどの構成要素よりも高いことが確認できる。次に,自己相関係数を計算してみよう。
df['tfp_cycle'].autocorr()
0.5381766486070036
gdp_cycle程ではないが、強い持続性があることが確認できる。
df['gdp_cycle'].autocorr()
0.6974503788747033
<これらの結果の含意>
全要素生産性の変動は大きく持続性も高い。またGDPとの相関性も大きい。これらから全要素生産性が景気循環を引き起こす要因ではないかということが示唆される。全要素生産性は資本や労働時間で説明できないGDPの要素であり,そのような「その他」の部分に景気循環を引き起こすランダムな要素が隠されているかも知れない,という考え方である。
労働時間とTFPの関係#
GDPと労働時間には正の相関があり、GDPとTFPにも正の相関がある。 では、労働時間とTFPにはどのような関係があるのだろうか。 散布図で確認してみよう。
df.plot.scatter(x='tfp_cycle', y='total_hours_cycle')
pass
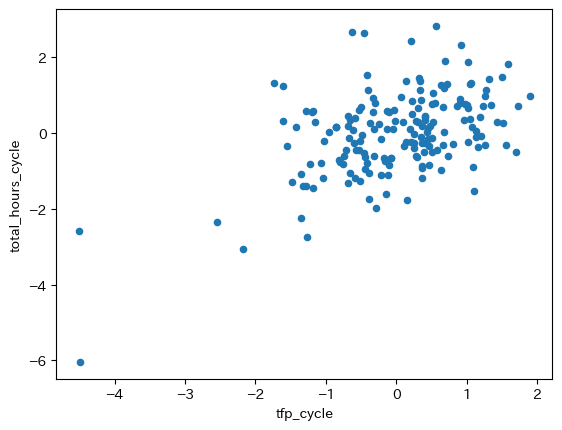
正のトレンドがある。相関係数を計算してみよう。
rho_tfp_total_hours = df[['total_hours_cycle', 'tfp_cycle']].corr().iloc[0,1]
rho_tfp_total_hours
0.5022784971433205
約0.5の値となっており、両変数ともGDPと正の相関があるため、驚くべき結果ではないかも知れない。
経済学的なメカニズムはどうだろうか?
この問は、通常の消費はの労働供給モデルを使うと簡単に理解できる。
TFPの上昇は実質賃金の上昇につながるが、次の2つの効果により消費者の労働供給は変化することになる。
代替効果:賃金の上昇は余暇の機械費用の上昇となるため、余暇を減らし労働供給を増やす。
所得効果:賃金の上昇は所得の増大であり、余暇を増やし労働供給を減らす。
労働時間とTFPの正の相関は、代替効果が所得効果を上回っていることを意味する。 この点は、TFPを景気循環の要素と考える場合に重要なポイントとなり、内生的労働供給の導入で詳細に議論することになる。
AR(1)としてのTFPと労働時間#
TFP#
全要素生産性を景気循環の要因として捉えるために,全要素生産性をAR(1)としてモデル化してみようというのがこの節の目的である。そのためにstatsmodelsを使い回帰分析をしてみよう。まず1期ずらした変数を作成する。
df['tfp_cycle_lag'] = df['tfp_cycle'].shift()
コードの説明
shift()はSeriesを1期ずらすメソッドである。
df[['tfp_cycle','tfp_cycle_lag']].head()
| tfp_cycle | tfp_cycle_lag | |
|---|---|---|
| 1980-01-01 | 0.403866 | NaN |
| 1980-04-01 | -1.195918 | 0.403866 |
| 1980-07-01 | -0.010875 | -1.195918 |
| 1980-10-01 | 1.132255 | -0.010875 |
| 1981-01-01 | 1.159067 | 1.132255 |
列tfp_cycle_lagは列tfp_cycleを1期ずらしていることが確認できる。次に回帰分析をおこなう。
res_tfp = smf.ols('tfp_cycle ~ -1 + tfp_cycle_lag', data=df).fit()
rho_tfp = res_tfp.params.iloc[0]
rho_tfp
0.5380002430152667
コードの説明
回帰式の中に-1とあるが、定数項を省く場合に指定する。
自己相関係数と殆ど変わらない値である。2つの変数の散布図を表示してみよう。
df.plot.scatter(x='tfp_cycle_lag', y='tfp_cycle')
pass
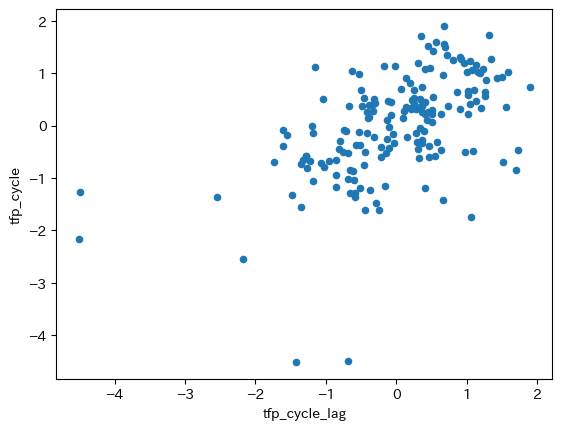
正の相関が図でも確認できる。次に\(\epsilon_t\)について考える。この変数はホワイト・ノイズであり、TFPショックの「源泉」である。平均0の正規分布としてモデル化するが,上の回帰式の残差の標準偏差をTFPの標準偏差の推定値として考えよう。
sigma_tfp = res_tfp.resid.std()
sigma_tfp
0.827072362021324
コードの説明
res_tfpの属性.residは残差を返している。.residはSeriesであり,その属性std()を使い標本標準偏差を計算している(デフォルトではddof=1)。
初期値は0としてrho_tfpとsigma_tfpを使ってAR(1)の値を計算してプロットしてみよう。
T = 120 # 標本の大きさ
A = 0 # 初期値
A_lst = [A] # 値を格納するリスト
for i in range(T):
e = np.random.normal(loc=0, scale=sigma_tfp)
A = rho_tfp * A + e
A_lst.append(A)
df_A = pd.Series(A_lst) # Seriesの作成
ax_ = df_A.plot() # 図示
ax_.axhline(0, c='red') # 0の平行線
ac_tfp = df_A.autocorr() # 自己相関係数の計算
print(f'TFPの自己相関係数:{ac_tfp:.3f}')
TFPの自己相関係数:0.427
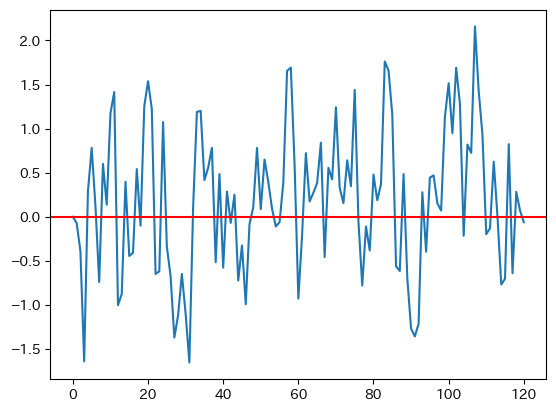
シミュレーションを行う度に図と自己相関係数は異なることになる。
労働時間#
労働時間にも同様の分析を行ってみよう。
# `1`期シフトした`total_hours_cycle`を作成
df['total_hours_cycle_lag'] = df['total_hours_cycle'].shift()
# AR(1)として単回帰分析
res_total_hours = smf.ols('total_hours_cycle ~ -1 + total_hours_cycle_lag', data=df).fit()
rho_total_hours = res_total_hours.params.iloc[0]
スロープ係数の推定値を表示し、散布図をプロットしよう。
rho_total_hours
0.5805663827193915
df.plot.scatter(x='total_hours_cycle_lag', y='total_hours_cycle')
pass
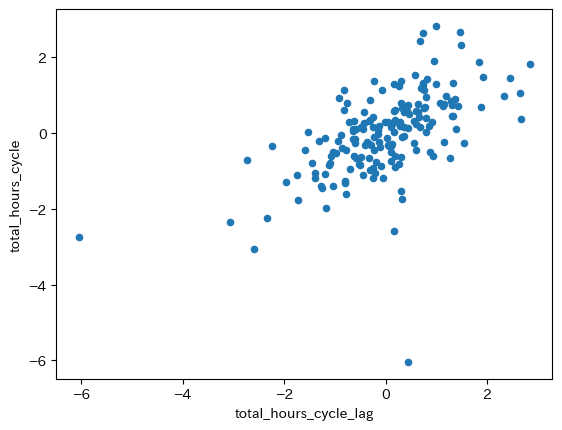
正の相関が確認できる。
要素分解====#
sigma2y = df['gdp_cycle'].var()
sigma2a = df['tfp_cycle'].var()
sigma2k = df['capital_cycle'].var()
sigma2h = df['total_hours_cycle'].var()
cov_ak = df[['tfp_cycle', 'capital_cycle']].cov().iloc[0,1]
cov_ah = df[['tfp_cycle', 'total_hours_cycle']].cov().iloc[0,1]
cov_kh = df[['capital_cycle', 'total_hours_cycle']].cov().iloc[0,1]
a = 0.36
# tfp contribution
tfp_contribution = ( sigma2a + a*cov_ak + (1-a)*cov_ah ) / sigma2y
capital_contribution = ( a**2*sigma2k + a*cov_ak + a*(1-a)*cov_kh ) / sigma2y
labour_contribution = ( (1-a)**2*sigma2h + (1-a)*cov_ah + a*(1-a)*cov_kh ) / sigma2y
print(tfp_contribution)
print(capital_contribution)
print(labour_contribution)
print(tfp_contribution + capital_contribution + labour_contribution)
0.5947705683721586
0.012642949037544933
0.3925864825861498
0.9999999999958533
a = 0.36
# tfp contribution
tfp_contribution = sigma2a / sigma2y
capital_contribution = a**2*sigma2k / sigma2y
labour_contribution = (1-a)**2*sigma2h / sigma2y
print(tfp_contribution)
print(capital_contribution)
print(labour_contribution)
print(tfp_contribution + capital_contribution + labour_contribution)
0.43559403307422173
0.007485581904457242
0.22919646097039098
0.67227607594907
# tfp contribution
tfp_contribution = sigma2a / sigma2y
capital_contribution = sigma2k / sigma2y
labour_contribution = sigma2h / sigma2y
print(tfp_contribution)
print(capital_contribution)
print(labour_contribution)
print(tfp_contribution + capital_contribution + labour_contribution)
0.43559403307422173
0.05775911963315773
0.5595616722909935
1.052914824998373
確率的ソロー・モデル#
説明#
上で日本のデータを使い全要素生産性のrhoとsigmaを計算しシミュレーションを行なったが,そのような全要素生産性の変動が景気循環の主な要因と考えるのがRBCモデルと呼ばれるものである。RBCモデルの詳細については後の章で検討するが,ここではその導入として次の点を考察する
AR(1)としてのTFPを組み込んだソロー・モデルを景気循環モデルとして考えシミュレーションをおこない,計算結果をデータと比べてどの程度整合性があるかを検討する。
モデルの均衡式として以下を使う。
生産関数:\(Y_t=A_tB_tK_t^aH^{1-a}\)
\(A_tB_t\)が全要素生産性
\(A_t\)は変動を捉える項
\[\begin{split} \begin{align*} \log(A_{t})&=\rho\log(A_{t-1})+\varepsilon_t \\ \varepsilon_t&\sim \textit{WH}(0,\sigma^2) \end{align*} \end{split}\]\(B_t\)はトレンドを捉える項
\[ B_t=B_0(1+g)^t \]\(H\)は一定と仮定する(この仮定によりTFPの効果のみを考察可能となる。)
資本の蓄積方程式:\(K_{t+1}=sY_t+(1-d)K_t\)
消費:\(C_t=(1-s)Y_t\)
投資(貯蓄):\(I_t=sY_t\)
これらの式から次の2式で\(K_t\)と\(A_t\)の値が計算できる。
変数の初期値を次のように仮定する。
\(A_0=1\)
\(K_0=\) 1980年の資本ストックの平均
\(H\)は次の値として一定とする。
\(H=\) 1980年の総労働時間の平均
パラメータの値を次を仮定する。
\(\rho\)と\(\sigma\)は上で計算した
rho_tfpとsigma_tfpの値\(g=\) 1980年から最後の年までの平均四半期成長率
\(s=\) 1980年から最後の年までのGDPに占める投資の割合の平均
\(d=0.025\):年率約10%を想定
\(a=0.36\):資本の所得割合
シミュレーションの結果を次の変数を含むDataFrameにまとめる。
\(Y\),\(C\),\(I\),\(K\),\(A\)の水準の系列
\(Y\),\(C\),\(I\),\(K\),\(A\)のトレンドの系列
\(Y\),\(C\),\(I\),\(K\),\(A\)の変動(サイクル)の系列
初期値の計算#
まずGDP,資本,総労働時間の1980年と2019年の平均を計算する。
var_lst = ['gdp', 'capital', 'total_hours'] #1
year_lst = [df.index[0].year, df.index[-1].year] #2
gdp_dic = {} #3
K_dic = {} #4
H_dic = {} #5
for yr in year_lst: #6
cond = ( df.index.year == yr) #7
mean = df.loc[cond, var_lst].mean() #8
gdp_dic[yr] = mean.iloc[0] #9
K_dic[yr] = mean.iloc[1] #10
H_dic[yr] = mean.iloc[2] #11
コードの説明
#1:3つの変数のリスト#2:平均を計算する年のリストであり,df.index[0].yearとdf.index[-1].yearはインデックスから最初と最後の年を抽出する#3:それぞれの年のGDPの平均を格納する辞書#4:それぞれの年の資本ストックの平均を格納する辞書#5:それぞれの年の総労働時間の平均を格納する辞書#6:year_lstに対してのforループ#7:df.indexの年がyrと同じ場合はTrueを返し,そうでない場合はFalseを返すSeriesをcondに割り当てる。#8:それぞれの年の行,var_lstにある列を抽出し平均を計算する。.mean()は列の平均を計算する。計算した平均は
Seriesとして返されるので,それを左辺にある変数meanに割り当てる。
#9:meanの0番目の要素をgdp_dicのキーyr(年)に対応する値をして設定する。#10:meanの1番目の要素をK_dicのキーyr(年)に対応する値をして設定する。#11:meanの2番目の要素をH_dicのキーyr(年)に対応する値をして設定する。
このコードの結果を確認してみよう。例えば,
gdp_dic
{1980: 273013.55, 2023: 560278.625}
キー・値の2つのペアがある。キー1980の値には1980年のGDPの平均が設定されており,同様に,もう一つのキー2023の値には2023年のGDPの平均が設定されている。従って,次のコードで1980年の値にアクセスできる。
gdp_dic[1980]
他の辞書も同様である。
なぜforループを使うのか。
上のコードでforループを使っているが,もし使わなければ次のようなコードになる。
var_lst = ['gdp', 'capital', 'total_hours']
mean1980 = df.loc['1980-01-01':'1980-10-01', var_lst].mean()
mean2019 = df.loc['2019-01-01':'2019-10-01', var_lst].mean()
gdp1980 = mean1980.iloc[0]
K1980 = mean1980.iloc[1]
H1980 = mean1980.iloc[2]
gdp2019 = mean2019.iloc[0]
K2019 = mean2019.iloc[1]
H2019 = mean2019.iloc[2]
同じようなコードが並んでいる。py4macroのデータがアップデートされて2020年までのデータが含まれることになったとしよう。forループを使うコードであれば2019を2020に一ヵ所だけ変更すれば良い(変更する必要もないコードを書くことも可能)。forループを使わないコードで何ヵ所修正する必要があるか数えてみよう。面倒と感じないだろうか。それに修正箇所が増えればbugが紛れ込む可能性が増えていく。
次に全要素生産性の平均四半期成長率を計算するためにdfの列名を確認しよう。
df.columns
Index(['gdp', 'consumption', 'investment', 'government', 'exports', 'imports',
'capital', 'employed', 'unemployed', 'unemployment_rate', 'hours',
'total_hours', 'inflation', 'price', 'deflator', 'gdp_trend_log',
'gdp_cycle', 'hours_trend', 'hours_cycle', 'employed_trend_log',
'employed_cycle', 'total_hours_trend_log', 'total_hours_cycle',
'capital_trend', 'capital_cycle', 'tfp_log', 'tfp_log_trend',
'tfp_cycle', 'tfp_cycle_lag', 'total_hours_cycle_lag'],
dtype='object')
gdpは0番目,capitalは6番目,total_hoursは11番目の列にある。この情報をもとに次のように計算しよう。
var_idx = [0,6,11] # 1
df0 = df.iloc[0,var_idx] # 2
df1 = df.iloc[-1,var_idx] # 3
# 4
B0 = df0['gdp'] / ( df0['capital']**a * df0['total_hours']**(1-a) )
# 5
B1 = df1['gdp'] / ( df1['capital']**a * df1['total_hours']**(1-a) )
no_quarters = len(df) # 6
g = ( B1/B0 )**( 1/no_quarters )-1 # 7
g
0.0024154776754650165
コードの説明
3つの変数の列インデックのリスト
最初の行で3つの変数だけを抽出し
df0に割り当てる。最後の行で3つの変数だけを抽出し
df1に割り当てる。最初の四半期の全要素生産性の計算
最後の四半期の全要素生産性の計算
四半期の数
平均四半期成長率の計算
次にGDPに対する投資の割合の平均を計算する。
s = ( df['investment'] / df['gdp'] ).mean()
s
0.21716704443145593
約22%が投資に回されている。
シミュレーション#
関数#
シミュレーションのコードを関数としてまとめよう。
def stochastic_solow(T=160, # 160=40*4 40年間の四半期の数
rho=rho_tfp,
sigma=sigma_tfp,
g=g,
s=s,
d=0.025,
a=a,
H=H_dic[1980], # 1980年平均に固定
K0=K_dic[1980],
B0=B0):
"""引数:
T: シミュレーションの回数
rho: AR(1)のパラメータ
sigma: ホワイト・ノイズ分散
g: TFPの平均四半期成長率
s: 貯蓄率
d: 資本減耗率
a: 生産関数のパラメータ(資本の所得割合)
H: 総労働時間
返り値
次の変数を含むDataFrame
GDP,消費,投資,資本ストック,全要素生産性の水準,トレンド,変動"""
# ========== A,B,Kの計算 ==========
# アップデート用変数、最初は初期値を設定
A = 1 #1
B = B0 #2
K = K0 #3
# 計算結果を格納するリスト
A_lst = [A] #4
B_lst = [B] #5
K_lst = [K] #6
# A,B,Kの時系列の計算
for t in range(1,T):
K = s * A*B * K**a *H**(1-a) + (1-d)*K #7
e = np.random.normal(0, scale=sigma) #8
A = A**rho * np.exp(e) #9
B = B0 * (1+g)**t #10
A_lst.append(A) #11
B_lst.append(B)
K_lst.append(K)
# ========== DataFrameの作成 ==========
df_sim = pd.DataFrame({'K':K_lst, #12
'A':A_lst,
'B':B_lst})
# ========== Y,C,Iの計算 ========== #13
df_sim['Y'] = df_sim['A'] * df_sim['B'] * df_sim['K']**a * H**(1-a)
df_sim['C'] = (1-s) * df_sim['Y']
df_sim['I'] = s * df_sim['Y']
# ========== トレンドとサイクルの計算 ==========
for v in ['K','A','Y','C','I']:
# ---------- レンドの計算 ---------- #14
df_sim[f'{v}_log_trend'] = py4macro.trend( np.log(df_sim[v]) )
# ---------- サイクルの計算 ---------- #15
df_sim[f'{v}の変動'] = 100 * ( np.log( df_sim[v] ) - df_sim[f'{v}_log_trend'] )
return df_sim
コードの説明
#1:forループでアップデートされるAの値を一次的に格納する。最初は初期値が入っている。#2:forループでアップデートされるBの値を一次的に格納する。最初は初期値が入っている。#3:forループでアップデートされるKの値を一次的に格納する。最初は初期値が入っている。#4:Aの値を格納する空のリスト。初期値が入っている。#5:Bの値を格納する空のリスト。初期値が入っている。#6:Kの値を格納する空のリスト。初期値が入っている。#7:右辺では(4)~(6)の値(A,B,K)を使い来期のKを計算し,その値を左辺のKに割り当てる。この瞬間に(6)のKがアップデートされる。#8:来期のホワイト・ノイズの値を生成しeに割り当てる。#9:右辺では(4)の値(A)を使い来期のAの値を計算し,その値を左辺のAに割り当てる。この瞬間に(4)のAがアップデートされる。#10:右辺では来期のBの値を計算し,その値を左辺のBに割り当てる。この瞬間に(5)のBがアップデートされる。#11:リスト(1)~(3)に来期値を追加する。#12:リスト(1)~(3)を使いDataFrameの作成#13:Y,C,Iを計算し新たな列としてDataFrameに追加#14:トレンドを計算し新たな列としてDataFrameに追加f-stringを使って新しく作る列名をK_trendのように_trendを追加する。
#15:トレンドからの乖離を計算し新たな列としてDataFrameに追加f-stringを使って新しく作る列名をK_cycleのように_cycleを追加する。
実行#
デフォルトの値でシミュレーションを行い、最初の5行を表示する。
df_sim = stochastic_solow()
df_sim.head()
| K | A | B | Y | C | I | K_log_trend | Kの変動 | A_log_trend | Aの変動 | Y_log_trend | Yの変動 | C_log_trend | Cの変動 | I_log_trend | Iの変動 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 850057.673739 | 1.000000 | 0.366461 | 272210.617761 | 213095.442439 | 59115.175322 | 13.646336 | 0.672329 | -0.154260 | 15.425952 | 12.357651 | 15.667990 | 12.112816 | 15.667990 | 10.830563 | 15.667990 |
| 1 | 887921.407217 | 0.434501 | 0.367346 | 120436.110181 | 94281.356090 | 26154.754091 | 13.686709 | 0.992940 | -0.137193 | -69.636437 | 12.391664 | -69.278978 | 12.146829 | -69.278978 | 10.864576 | -69.278978 |
| 2 | 891878.126128 | 0.895705 | 0.368233 | 249272.367145 | 195138.623913 | 54133.743231 | 13.727086 | -2.600146 | -0.120031 | 0.988656 | 12.425775 | 0.052604 | 12.180939 | 0.052604 | 10.898687 | 0.052604 |
| 3 | 923714.916206 | 0.568798 | 0.369123 | 160693.651374 | 125796.286046 | 34897.365328 | 13.767478 | -3.131920 | -0.103111 | -46.111920 | 12.459649 | -47.239412 | 12.214813 | -47.239412 | 10.932561 | -47.239412 |
| 4 | 935519.408628 | 1.104966 | 0.370015 | 314356.513647 | 246088.638680 | 68267.874966 | 13.807878 | -5.902130 | -0.086765 | 18.657963 | 12.492951 | 16.533196 | 12.248115 | 16.533196 | 10.965863 | 16.533196 |
\(Y\)の水準とトレンドの図示(対数)。
np.log( df_sim['Y'] ).plot(title='シミュレーション:Yとトレンド(対数)')
df_sim['Y_log_trend'].plot()
pass
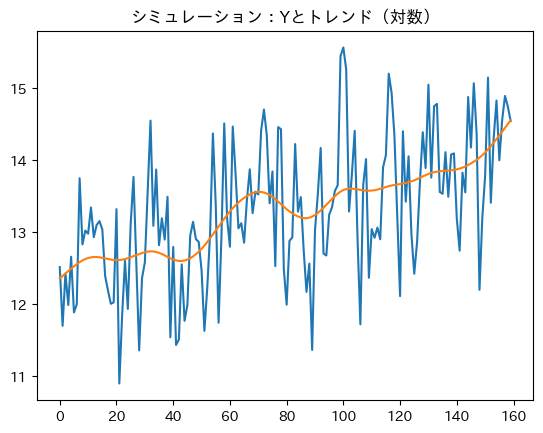
トレンドの傾きは成長率を表しているが,徐々に減少していることが分かる。最初は成長率に対する資本蓄積の効果が大きいが,定常状態に近づくにつれて資本蓄積の効果が減少しているためである。
\(Y\)の変動(サイクル)の図示。
ax_ = df_sim.plot(y='Yの変動', title='シミュレーション:Yの変動(%)')
ax_.axhline(0, c='red')
pass
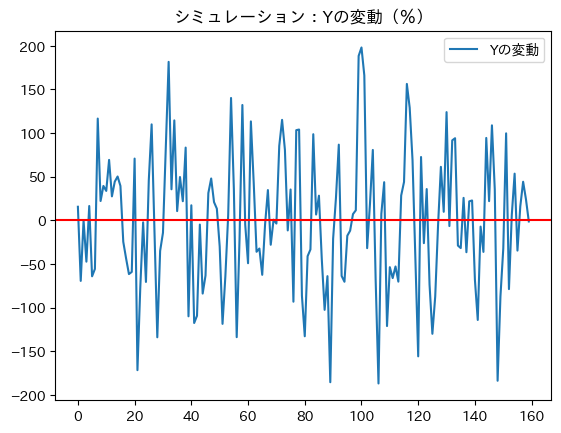
絶対値で概ね2%内に収まった変動となっている。データでは,リーマンショック時はマイナス約4%程乖離したが,それ以外は絶対値で2%以内に収まっており,シミュレーションは概ねデータと同じような特徴を持っていると言える。
結果1:自己相関#
それぞれの変数の自己相関係数を計算してみる。
var_lst = ['Y', 'C', 'I', 'K', 'A']
print('\n--- シミュレーション:変動の自己相関係数 ---\n')
for v in var_lst:
ac = df_sim[f'{v}の変動'].autocorr()
print(f'{v}の変動: {ac:.3f}')
--- シミュレーション:変動の自己相関係数 ---
Yの変動: 0.275
Cの変動: 0.275
Iの変動: 0.275
Kの変動: 0.856
Aの変動: 0.273
まずシミュレーションを行う度にこれらの値は変化することに留意し結果を考えよう。ある程度の自己相関が発生しており,\(A\)の影響が反映されている。\(Y\),\(C\),\(I\)の値は同じなのは,\(C\),\(I\)は\(Y\)の線形関数であるためであり,これらの3つの変数は\(A\)の変動と似た動きになっている。また\(K\)の値が大きいのは、ストック変数であるため変化に時間が掛かることが反映されているためである。
シミュレーション結果を評価するためにデータと比べる必要がある。
dfに含まれる日本のデータを使って自己相関係数を計算してみよう。まず消費,投資,資本の変動を計算する。
data_var_lst = ['consumption','investment','capital']
for v in data_var_lst:
df[f'{v}_cycle'] = np.log( df[v]/py4macro.trend(df[v]) )
結果を示すために,data_var_lstの最初と最後にgdpとtfpを追加する。
data_var_lst = ['gdp']+data_var_lst+['tfp']
print('\n--- データ:変動の自己相関係数 ---\n')
for v in data_var_lst:
ac = df[f'{v}_cycle'].autocorr()
print(f'{v:>11}の変動: {ac:>5.3f}') # 1
--- データ:変動の自己相関係数 ---
gdpの変動: 0.697
consumptionの変動: 0.493
investmentの変動: 0.838
capitalの変動: 0.953
tfpの変動: 0.538
コードの説明
f-stringを使って変数vとacを代入している。:>11はvを表示する幅を11に設定し右寄せ(>)にしている。:>5はacを表示する幅を5に設定して右寄せ(>)にしている。.3fはacを小数点第三位までを表示するように指定している。
実際の資本ストックは非常に大きな持続性があり、シミュレーションの結果はそれを捉えている。しかし他の変数、特に投資に関しては持続性が足りないようである。
しかしシミュレーションの結果はランダム変数の実現値に依存しているので,シミュレーションを行う度に異なる結果が出てくる。また,このシミュレーションではT=160として40年間を考えたが,Tの値によっても結果は大きく左右される。Tを大きくするとより安定的な結果になっていくだろう。例えば,T=10_000を試してみよう。
結果2:GDPとの相関#
次に、\(Y\)との相関係数を計算する。
print('\n--- シミュレーション:GDPとの相関係数 ---\n')
for v in var_lst[1:]:
cov = df_sim[['Yの変動',f'{v}の変動']].corr().iloc[0,1]
print(f'{v}の変動: {cov:.3f}')
--- シミュレーション:GDPとの相関係数 ---
Cの変動: 1.000
Iの変動: 1.000
Kの変動: -0.159
Aの変動: 1.000
\(C\)と\(I\)の値は1.0となっている理由は\(Y\)と線形になっているためであり,全く同じように変動するためである。
\(Y\)と\(A\)は非常に強く相関している。生産関数を見ると,両変数も線形の関係があり,\(K\)の変化によって変化のズレが生じるメカニズムとなっているためである。
シミュレーション結果ををデータと比べてみよう。
print('\n--- データ:GDPとの相関係数 ---\n')
for v in data_var_lst[1:]:
cor = df[['gdp_cycle',f'{v}_cycle']].corr().iloc[0,1]
print(f'{v:>11}の変動:{cor:>5.3f}')
--- データ:GDPとの相関係数 ---
consumptionの変動:0.767
investmentの変動:0.783
capitalの変動:0.131
tfpの変動:0.901
\(C\)と\(I\)に関してはシミュレーションの相関係数は大きすぎる結果となっている。
総評#
確率的ソロー・モデルによるシミュレーション結果は,マクロ変数の特徴を捉えている部分もあるが景気循環モデルとして考えるには難しいだろう。消費者の効用最大化問題が欠落しているため,\(Y\),\(C\),\(I\)が全く同じように動くのがネックになり,消費や投資の特徴を捉えることができていない。後の章で議論するが,消費者の最適化問題や将来の予測などを導入したRBCモデルは,よりデータに近い結果となる。しかし,いくつか問題が残るのも事実である。
TFPショックとは何なのか?
生産関数を見る限りTFPは生産性を表している。技術水準,政府の規制,政治システムや経済制度の変化を捉えると考えられ,例えば,ビジネスに対する規制の強化によって負のショックが発生する。しかし,それだけで実際に観測されるGDPの大きな変動(例えば、リーマン・ショックやコロナ・ショック)を説明するのには疑問である。
ソロー・モデルも含めて価格調整が瞬時に行われるが,次の問題が残る。
古典派の二分法が成立すると仮定するが、短期的には無理がある仮定(例えば、賃金)。
景気循環に対して金融政策は無力なのか?
このような問題意識を持って,RBCモデルとニューケインジアン・モデルを議論していくことにする。

