差分方程式と経済分析#
import japanize_matplotlib
import numpy as np
import pandas as pd
import statsmodels.formula.api as sm
# numpy v1の表示を使用
np.set_printoptions(legacy='1.21')
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
はじめに#
この章ではまず第一に,動学モデルの基礎(の基礎)を理解することである。マクロ経済は時間を考慮せざるを得ない。経済成長,インフレ,デフレ,景気循環などは全て時間軸に沿って考える必要がある。マクロ経済では変数の変化が重要な役割を果たすためである。そして時間と密接に関係するのがpersistenceと呼ばれるマクロ変数の特徴である。persistenceとは,マクロ変数が一度ある状態に陥ると,その状態が継続する傾向にある性質を指す。典型的な例がデフレである。日本はデフレからなかなか脱却できないが,それがデフレのpersistenceである。これは前期の影響が今期に,今期の影響が来期に現れることによって発生する。時間という概念から離れてpersistenceを考えるのは難しい。一方で,時間を扱う「動学」と聞くと難しく感じるかもしれないが,構える必要はない。高校数学で習った漸化式(以下では「差分方程式」を同義として扱う)を使うが,解法テクニックが重要ではなく,漸化式の考え方を捉えるコードを書き,後はPythonが計算することになる。
1階差分方程式#
説明#
差分方程式(漸化式)とは,初期の値を所与として値の数列を定義する方程式である。言い換えると,\(t\)期の変数の値は\(t-1\)期やそれ以前の値に依存する関係を表す式である。例を考えよう。
\(x_0\)は与えられていると仮定しよう。連続して代入する(逐次代入法)。
このことから次のことがわかる。
\(t\rightarrow\infty\)とすると(\(x_0\ne 0\))
\(a=1\)の場合
\(b=0\)の場合,\(x_t\)は同じ値\(x_0\)にとどまる。
\(b>0\)の場合,\(b\sum_{i=0}^ta^i=b(1+t)\rightarrow\infty\)となり\(x_t\)は発散する。
\(b<0\)の場合,\(b\sum_{i=0}^ta^i=b(1+t)\rightarrow-\infty\)となり\(x_t\)は発散する。
\(a=-1\)の場合
\(b\)の値に関わらず,\(x_t\)は振動する。
\(a>1\)の場合,\(a^{t+1}\rightarrow\infty\)となり\(x_t\)は正の無限大に発散する。
\(a<-1\)の場合,\(x_t\)は振動し\(a^{t+1}\rightarrow\infty\)もしくは\(-\infty\)となり発散する。
\(|a|<1\)の場合\(x_t\)は収束
\(0<a<1\)の場合は単調的に収束
\(-1<a<0\)の場合は振動し収束
\(a^{t+1}x_0\rightarrow 0\)
\(\sum_{i=0}^ta^t\)は\(S\)に収束する。
\[\begin{split} \begin{align*} S&=\sum_{i=0}^{\infty}a^t=1+a+a^2+a^3+\cdots \\ aS&=a+a^2+a^3+\cdots \\ S-aS&=1 \\ &\Downarrow \\ S&=\dfrac{1}{1-a} \end{align*} \end{split}\]\(t\rightarrow\infty\)の場合の\(x_t\)の値を\(x_{*}\)としよう。\(t\rightarrow\infty\)の下では\(x_t=x_{t-1}\equiv x_{*}\)となるため以下が成立する。
\[ x_{*}=ax_{*}+b \quad \Rightarrow \quad x_{*}=\dfrac{b}{1-a}=bS \]
均衡を考える上で\(x_t\)が発散するケースは除外し,収束するケースに着目する。
例1#
初期値:\(x_0=1\)
(22)#\[ x_{t+1}=0.4x_{t}+3 \]\(0.4<1\)なため収束することが分かる。
定常状態は次の値となる。
\[ x_{*}=0.4x_{*}+3 \quad\Rightarrow\quad x_{*}=\dfrac{3}{1-0.4}=5 \]
ここでまとめたことはFig. 2から確認できる。
① 初期を\(x_0<5\)(例えば,1)とする。
② \(x_0\)を所与として式(22)の右辺によって\(x_1\)が決まる。
③ \(x_1\)を縦軸で確かめる。
④ ③から平行移動した45度線上の点
⑤ ④から垂直に降りて横軸に\(x_1\)を確認できる。
⑥ \(x_1\)を所与として式(22)の右辺によって\(x_2\)が決まる。
⑦ \(x_2\)を縦軸で確かめる。
⑧ ⑦から平行移動した45度線上の点
⑨ ⑧から垂直に降りて横軸に\(x_2\)を確認できる。
このプロセスのリピートし最終的に定常状態(\(x_t=x_{t+1}\))に収束する
この場合の定常状態を「安定的(stable)」と呼ぶ。ここで覚えて欲しいことは,まず第一に式(22)と45度線の交点が定常状態である。そして45度線の傾きは1に対して式(22)の傾きは0.4なので,式(22)は「上から」45度線と交わっている。
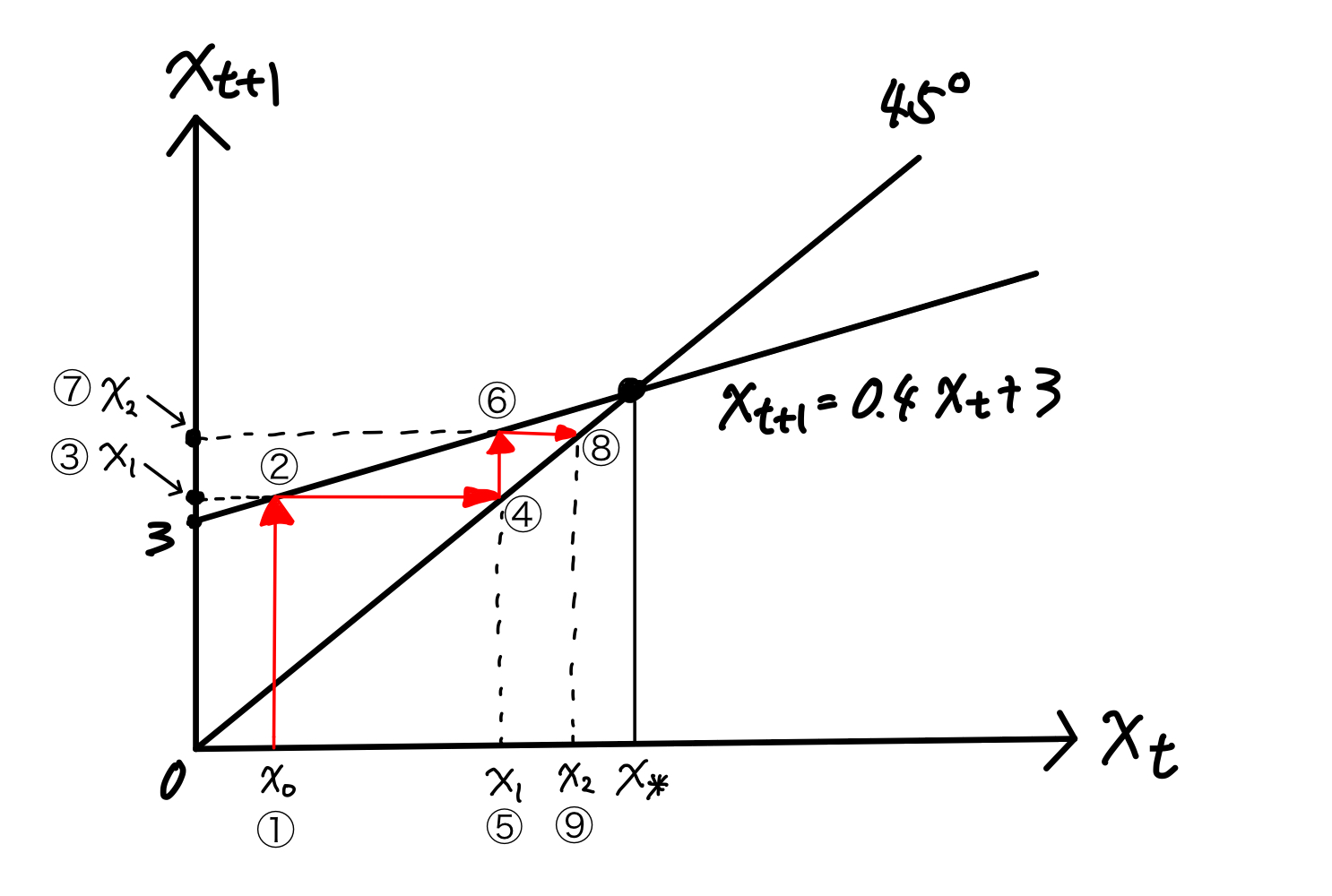
Fig. 2 例1#
次にコードを書いて\(x_t\)を計算しプロットするが,3つの方法を紹介する。
方法1#
計算した\(x\)の値を一時的に割り当てるアップデート用の変数を使う方法を考える。この方法は,下で説明する方法1と2よりもPython的(Pythonic)な方法であり,一番オススメの方法である。
x = 1 # 1
x_lst = [x] # 2
for i in range(20):
x = 0.4 * x + 3 # 3
x_lst.append(x) # 4
コードの説明
xはアップデート用の変数として使う。初期値は1。初期値が入ったリストであり、このリストに計算結果を追加する。
来期の
xの計算1回目のループ:右辺では(1)で設定した
xの初期値を使い計算し,結果を左辺のxに割り当てる。この時点で,(1)のxは(3)の左辺のxと同じ変数なので,同じ計算結果が割り当てられアップデートされる。2回目以降のループ:右辺では
xの最新の値を使い計算し,結果を左辺のxに割り当てる。この時点,(1)のxは(3)の左辺のxと同じ変数なので,同じ計算結果が割り当てられアップデートされる。
(3)の左辺の
xを(2)のリストに追加する。
次にx_listをプロットするが,ここではDataFrameのメソッド.plot()を使う図示の方法を説明する。非常に簡単であり,DataFrameをdfとすると次の構文となる。
df.plot()
これだけでプロットが表示される。
まずDataFrameを作成しよう。様々な作成方法があるが,以下では辞書を使う方法を紹介する。辞書のキーが列ラベルになり,値が列の値となる。
df = pd.DataFrame({'X':x_lst})
df.head()
| X | |
|---|---|
| 0 | 1.0000 |
| 1 | 3.4000 |
| 2 | 4.3600 |
| 3 | 4.7440 |
| 4 | 4.8976 |
では図示してみよう。
df.plot()
pass
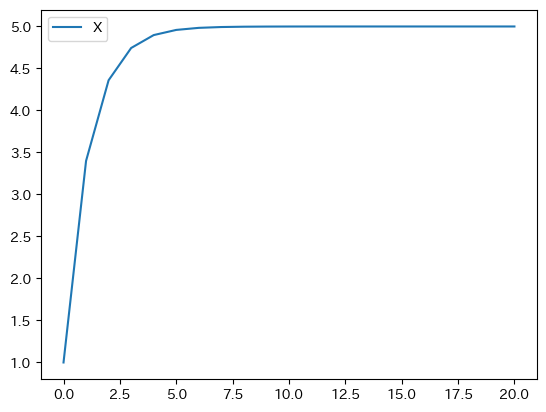
この図の縦軸は\(x_t\)であり,横軸は行インデックスがfloatとして表示されており,ループの回数と同じ(自動表示なので整数となる場合もある)。強制的に横軸に整数を表示したい場合はdf.plot()の代わりに次のコードを使えば良いだろう。
ax_ = df.plot()
ax_.set_xticks(range(21))
コードの説明
1行目:
.plot()で生成される「軸」をax_に割り当てる。2行目:
ax_のメソッド.set_xticksは横軸の目盛を設定し,引数には使う目盛を指定する。range(21)を使うことで0から10の全ての整数を指定しているが,range(0,11,2)にすれば0,2,4,6…といった表示も可能である。
方法2#
この方法では,値を格納するために使うリストを使うが、その中にある値を直接forループの中で使う。
x_lst = [1] # 1
for i in range(20):
x = 0.4 * x_lst[i] + 3 # 2
x_lst.append(x) # 3
pd.DataFrame({'X':x_lst}).plot()
pass

主なコードの説明
初期値が入ったリストを用意する。
リストの中にある
i番目の値を使い右辺を計算しxに割り当てる。(2)で計算した
xの値をリストに追加する。
方法3#
1(初期値)と計算する回数分のNumpyのarrayを用意し、計算結果をその中に格納する。
n = 20 # 1
arr = np.zeros(1+n) # 2
arr[0] = 1 # 3
for i in range(n):
arr[i+1] = 0.4 * arr[i] + 3 # 4
pd.DataFrame({'X':arr}).plot()
pass

コードの説明
ループの回数
np.zeros()は引数の数だけ0が並ぶarrayを作成する関数。1+nの1は(3)で初期値を代入するために必要となる。arrの0番目に初期値を代入する。右辺では
arrのi番目の値を使い来期の値を計算し,=を使いarrのi+1番目に代入する。
例2#
\(1.2>1\)なため発散する。
定常状態の値を計算する。
\[ x_{*}=1.2x_{*}-0.2 \quad\Rightarrow\quad x_{*}=\dfrac{0.2}{1.2-1.0}=1 \]
この結果はFig. 3を使って確認できる。図の読み方は例1と同じである。式(23)は「下から」45度線を交差している。初期値を\(x_0=1.1>x_*\)として発散することを示しているが,\(x_0<1\)の場合でも発散することになる(試してみよう)。この場合の定常状態\(x_*\)は「不安定(unstable)」と呼ぶ。
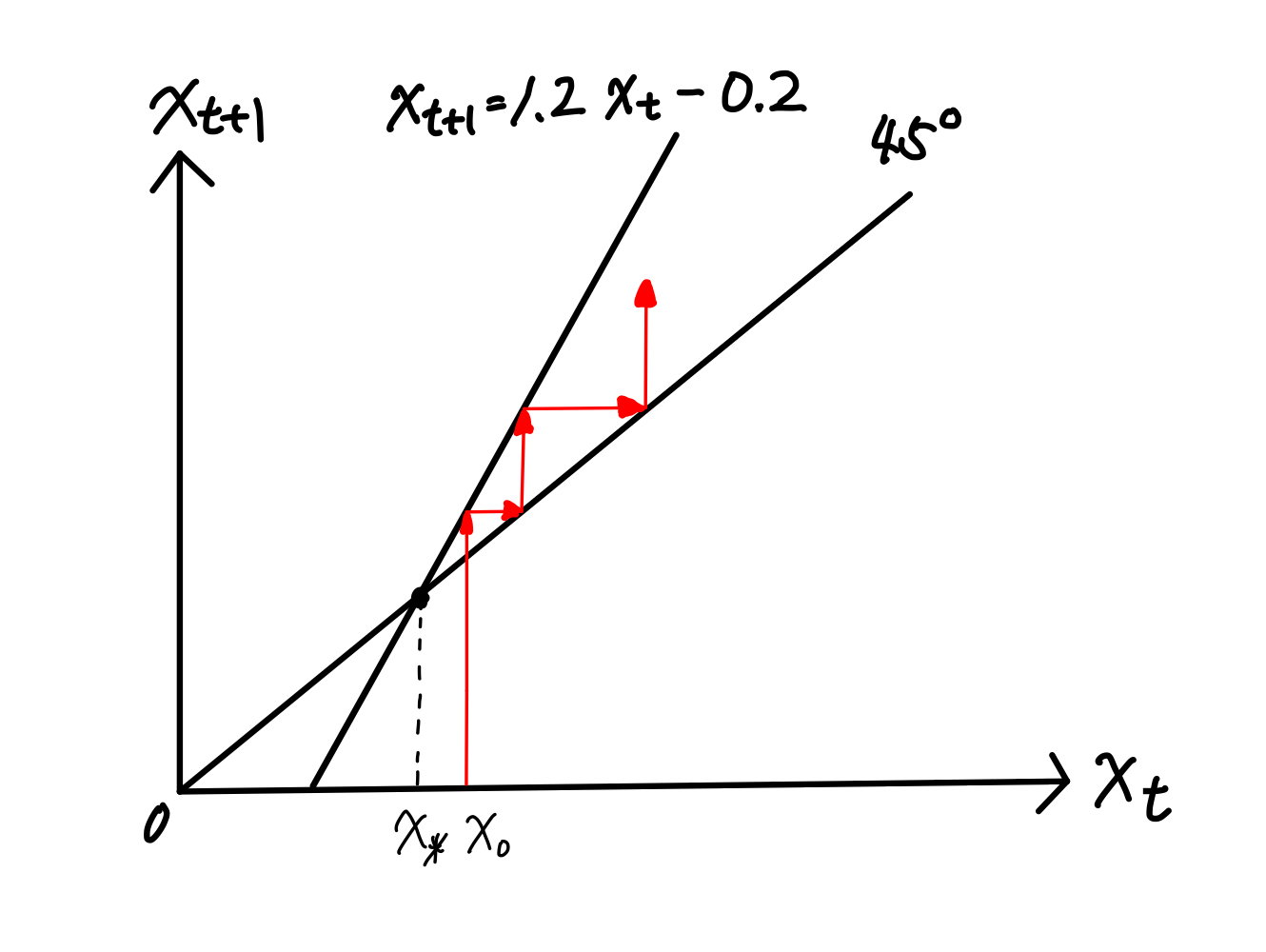
Fig. 3 例2#
x = 1.1 # 初期値 x0
x_lst = [x]
for i in range(50):
x = 1.2 * x - 0.2
x_lst.append(x)
pd.DataFrame({'X':x_lst}).plot()
pass
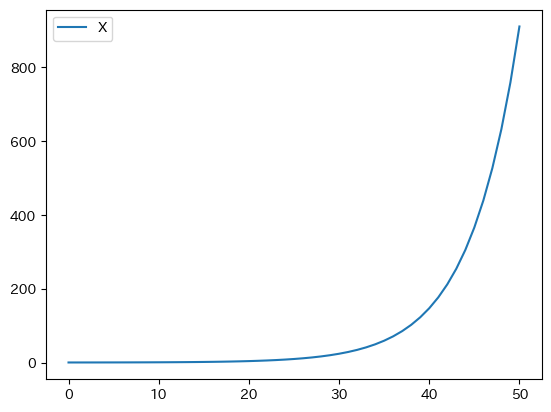
例3#
この式は上の例と違って非線形の差分方程式となっている。しかし,数値計算のためのPythonコードに関しては大きな違いはない。単に,コードの中で非線形の式を書くだけで良い。しかし収束か発散かの安定性(stability)を解析的に確認するには,定常状態の近傍を考える必要がある。基本的なアイデアは次のようなものである。定常状態に非常に近い周辺を考えよう。十分に定常状態に近ければ、非線形差分方程式は線形に非常に近くなる。例えば、地球は丸いが、その上で暮らす小さな人間にとって大きな地球は平らに感じる。これは無意識に線形近似を行なっているのと同じである。この考えを使い、非線形差分方程式を定常状態の周りで線形近似することで,あたかも線形の様に考えて安定性を確認できる。手法としてはテイラー展開を使い線形近似する。
<テイラー展開による1次線形近似>
関数\(y=f(k)\)を\(k_{*}\)でテイラー展開すると次式となる。
\[ y=f(k_{*})+\left.\frac{df}{dk}\right|_{k=k_{*}}(k-k_{*}) \]
(24)に当てはめると次のような対応関係にある。
\(y\;\Rightarrow\;x_{t+1}\)
\(f(k)\;\Rightarrow\;ak_{t}^{0.5}\)
\(k_{*}\;\Rightarrow\;x_{*}\)
テーラー展開する前に,\(x_{*}\)を計算してみよう。(24)で\(x_{t+1}=x_{t}=x_{*}\)とすると
これらを使い,(24)をテーラー展開すると
となる。\(0.5<1\)なので収束することが確認できた。また,定常状態も次のように計算できる。
図示するとFig. 4の様になる。
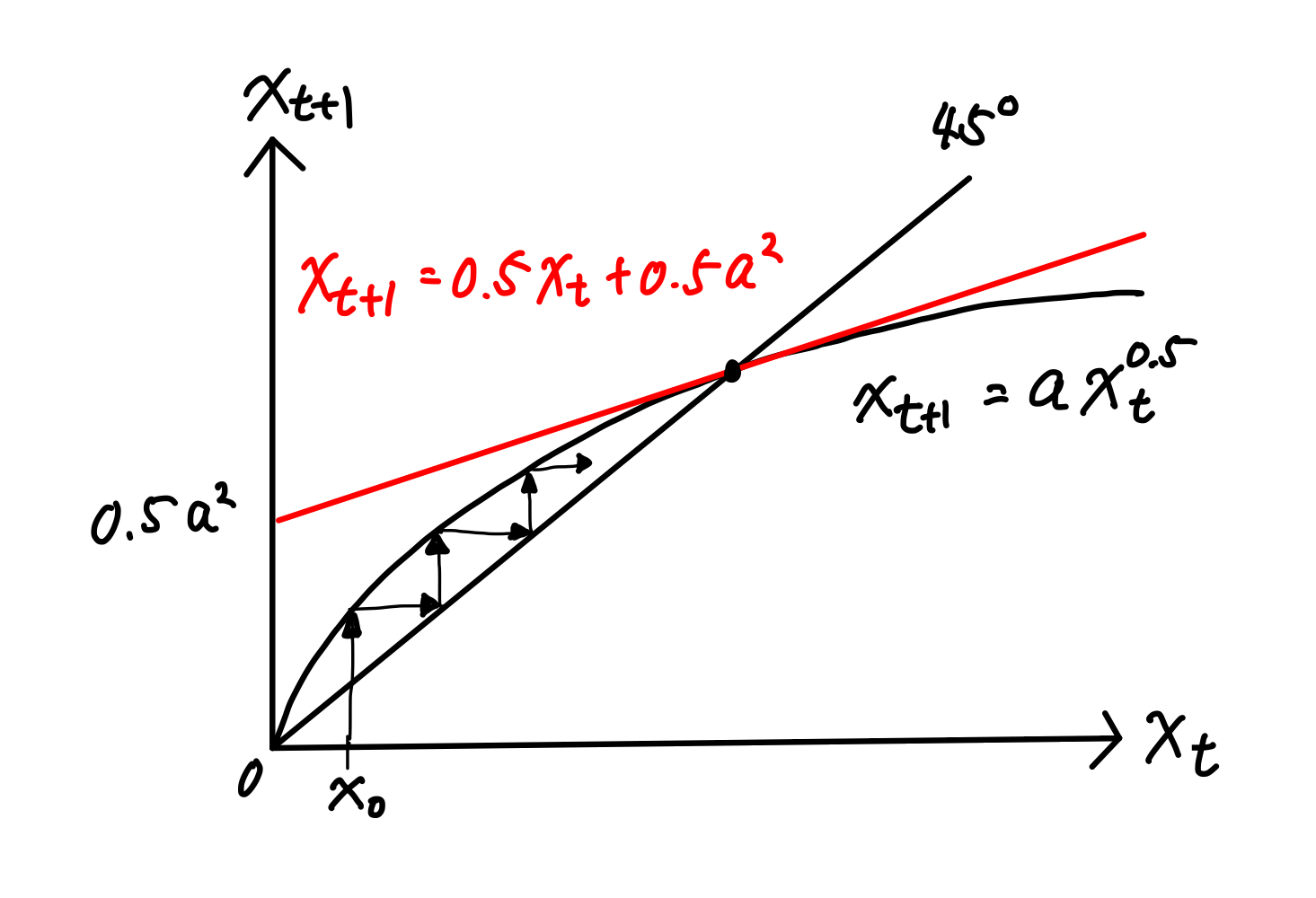
Fig. 4 例3#
差分方程式が45度線近傍で増加関数の場合はもっと簡単な判定方法がある。
縦軸に\(x_{t+1}\),横軸に\(x_t\)の図で差分方程式が45度線と
「上から交差」する場合,\(x_t\)は定常値へ収束する(定常状態は安定的)
「下から交差」する場合,\(x_t\)は発散する(定常状態は不安定)
\(a=2\)としてコードを書いて実行してみよう。
x = 3.5 # 初期値 x0
x_lst = [x]
for i in range(20):
x = 2 * x ** 0.5
x_lst.append(x)
pd.DataFrame({'X':x_lst}).plot()
pass
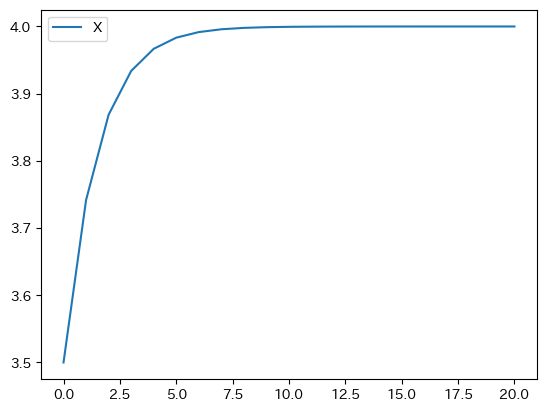
例4#
次の非線形差分方程式を考えてみよう。
数値計算をせずとも,\(0<b<1\)の場合は上の式は45度線と「上から交差」するため安定的であることは直ぐにわかる。 定常状態\(x_{*}\)は
で定義されるが,解を明示的に求めることはできない。 しかし,数値計算で\(x_t\)の値は簡単に計算できる。
初期値x0,パラメータa,forループ計算関数nを引数として,関数を作成して確かめよう。
def my_dynamics(x0, a, b, n):
x = x0
x_lst = []
for _ in range(n):
x = a * x**b + 10
x_lst.append(x)
return pd.DataFrame({'X': x_lst})
my_dynamics(x0=40, a=1, b=0.9, n=5)
| X | |
|---|---|
| 0 | 37.660116 |
| 1 | 36.199529 |
| 2 | 35.283234 |
| 3 | 34.706518 |
| 4 | 34.342767 |
\(0<b<1\)のケースをプロットしてみよう。
my_dynamics(x0=40, a=1, b=0.9, n=20).plot(marker='o')
pass

\(b>1\)のケースをプロットしてみよう。
my_dynamics(x0=40, a=1, b=1.1, n=15).plot(marker='o')
pass
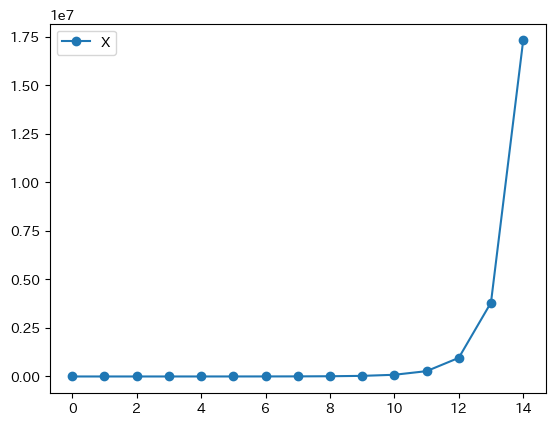
45度線モデル#
マクロ経済学の基本モデルとなるケインズの45度線モデルを考えてみる。次の仮定を置く。
所得恒等式:\(y_t=c_t+inv_t\)
消費:\(c_t=a+by_t\)
\(a>0\):所得とは独立した消費
\(0<b<1\):限界消費性向
投資:\(inv_t=d+fy_{t-1}\)
\(t\)期の投資は前期である\(t-1\)期の産出量に依存すると仮定する。工場を建てたりするには時間が掛かる様に投資計画を実行するには時間を要することを捉えている。この仮定により産出量の動学的な動きが発生する事になる。
\(f>0\):前期の産出量に依存する投資
\(d>0\):産出量に依存しない投資
均衡式:\(y_t=a+by_t+d+fy_{t-1}\)
均衡式を1期進めると次式となる。
この式から次のことが分かる。定常状態の安定性は\(\dfrac{f}{1-b}\)に依存しており,パラメータの値から定常状態は安定的であり,初期値\(y_0\)から収束することになる。定常状態を計算しよう。実質変数である\(y_t\)が一定になる状態なので次式が成立する。
定常状態で\(y_*>0\)が成立してこそ意味があるので,\(1>b+f\)を仮定しよう。モデルの動学を図示したのがFig. 5である。
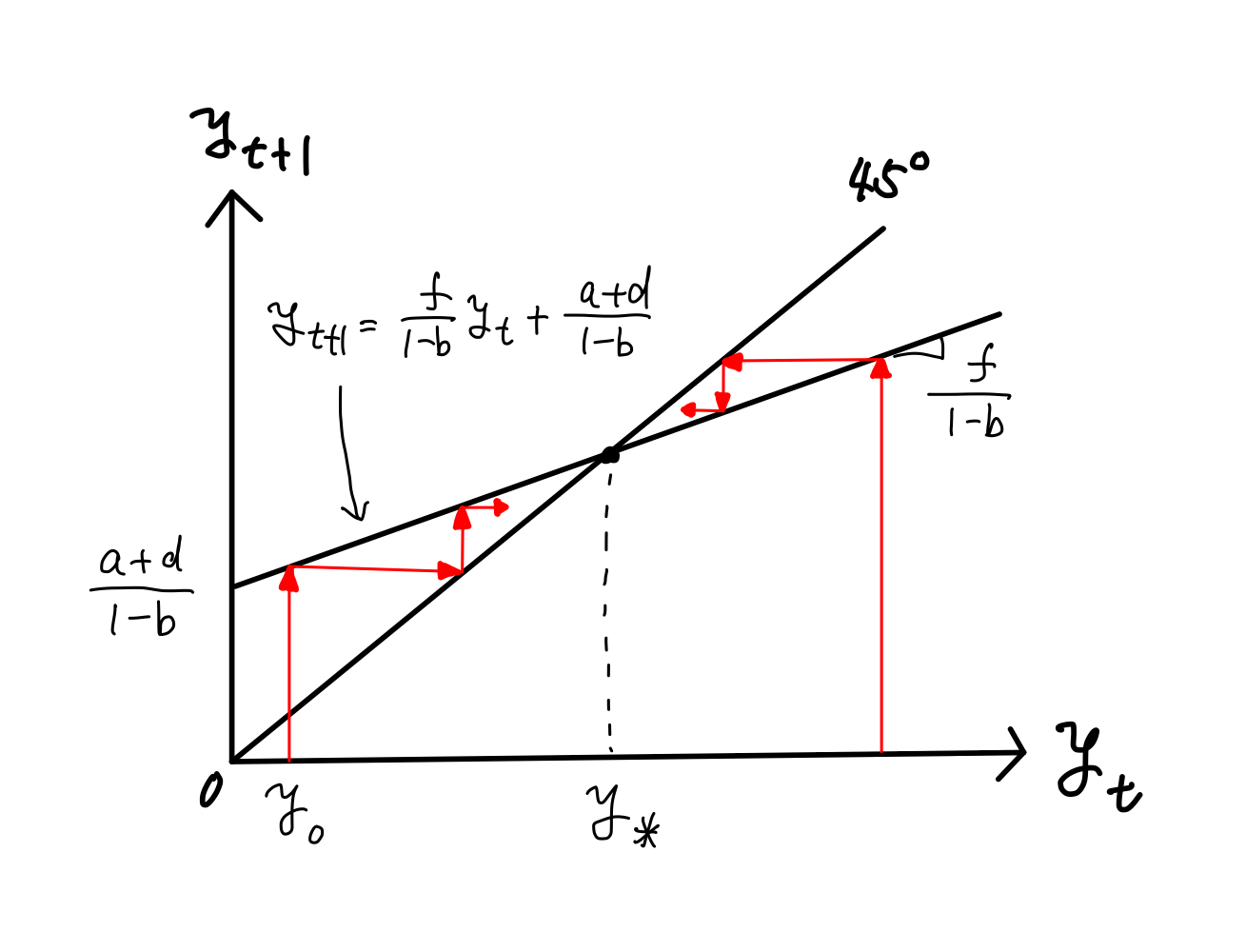
Fig. 5 45度線モデル#
次に,実際にコードを書いて\(y_t\)の動学的な動きを確認してみよう。次の関数を定義する。
def model45(y0, a, b, d, f, n=10):
"""引数 #1
y0: GDPの初期値
a: 所得に依存しない消費
b: 限界消費性向
d: 産出量に依存しない投資
f: 前期の産出量に依存する投資
n: ループの回数(デフォルト10)
戻り値
yの値からなるDataFrame"""
y = y0 #2
y_lst = [y0] #3
for i in range(n):
y = y * f / (1-b) + (a+d) / (1-b) # 4
y_lst.append(y) # 5
yss = (a+d) / (1-b-f) # 6
print(f'定常状態での産出量:{yss:.1f}') # 7
return pd.DataFrame({'output':y_lst}) # 8
コードの説明
"""と"""で挟んだ領域はdocstringと呼ばれ、関数の説明をする。書かなくても良いが、自分が忘れた頃に関数のコードを読むことになるかも知れないので、書く方がオススメ。yはアップデート用の変数であり,初期値y0をyに割り当てる。初期値が入ったリストであり,
forループで計算するyを格納する。右辺の
yは(1)のyであり,右辺の計算結果を左辺のyに割り当て(1)のyの値をアップデートする。(3)で計算した
yの値をy_listに追加する。定常状態
yssを計算する。定常状態の値を表示する。
:.1fは小数点第一位まで表示することを指定する。DataFrameを作成し,関数が実行されるとそれを返す。
model45(100, a=50, b=0.5, d=50, f=0.2).plot()
pass
定常状態での産出量:333.3
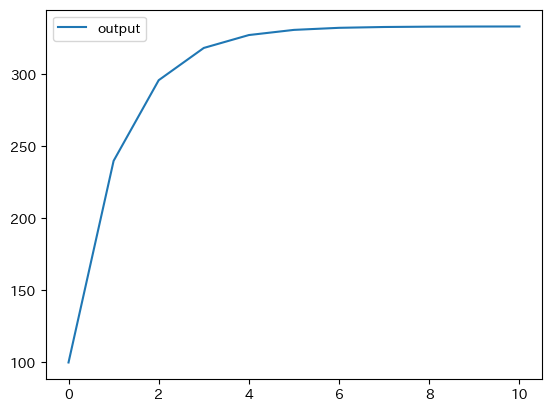
コードの説明
model45()の返り値はDataFrameである。そのメソッド.plot()を直接使って図示している。
初期値は定常状態の値よりも低く設定されているため,産出量は徐々に増加することになる。初期値を定常状態の値よりも大きい場合どうなるか確認してみよう。
蜘蛛の巣モデル#
もう一つの簡単な経済モデルを取り上げる。需要と供給モデルであり,均衡では価格と財の量が決定される。
需要曲線
消費者は今期の価格に基づいて今期の需要を決める。
\[ d_t = a - bp_t,\quad a,b>0 \]
供給曲線
生産者は価格を観察し生産量を決めるが,その決定は1期前の価格に依存すると仮定する。例えば,農家が想定できる。種を植え収穫し市場に供給するまで時間が掛かることを\(p_{t-1}\)が捉えている。
\[ s_t = -c + dp_{t-1},\quad c,d>0 \]\(t\)期の供給量が\(t-1\)期の価格に依存することにより,動学的な動きが発生する事になる。
均衡条件
\[ d_t=s_t\equiv q_t \]
均衡式を1つにまとめる。
この式から定常状態の安定性が簡単に確認できる。均衡が収束するのか発散するのかは需要と供給の価格の係数,言い換えると,需要と供給がどれだけ価格に反応するかに依存していることが分かる。この結果を需要曲線と供給曲線の傾きで表すために次のこと確認しよう。
収束:\(\dfrac{d}{b}<1\)もしくは\(\dfrac{1}{b}<\dfrac{1}{d}\)
需要曲線と比べて供給曲線の傾きが大きい場合に長期均衡に収束する。
発散:\(\dfrac{d}{b}>1\)もしくは\(\dfrac{1}{b}>\dfrac{1}{d}\)
需要曲線と比べて供給曲線の傾きが小さい場合に発散する。
2期間サイクル:\(\dfrac{d}{b}=1\)
式(26)を使うと定常状態(長期的均衡)の価格は次のように計算できる。
また定常状態の量は需要曲線もしくは供給曲線を使って計算する。
Fig. 6は価格\(p_t\)の動学を示している。需要曲線に比べて供給曲線がより急な傾きになっているため定常状態に収束している。その逆の場合は発散することになるので図を描いて確かめてみよう。
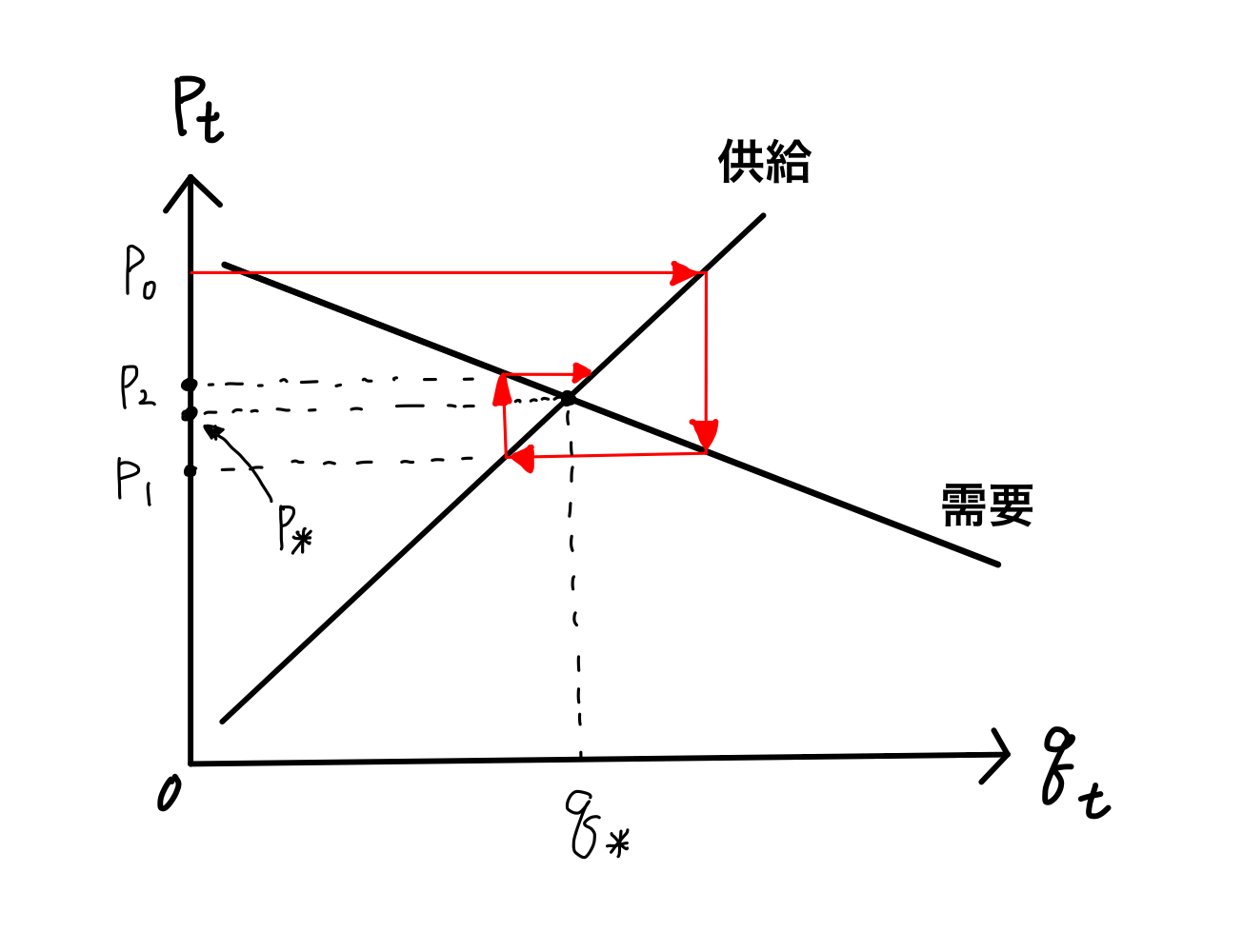
Fig. 6 蜘蛛の巣モデル(モデル名は均衡の軌跡が蜘蛛の巣に似てるため)#
次にコードを書いて価格と量の動学を確かめるが,45度線モデルと同じように関数を作りプロットする。
def cobweb(p0, a, b, c, d, n=10):
"""引数
p0: 初期値
a: 需要曲線の切片
b: 需要曲線の傾き
c: 供給曲線の切片
d: 供給曲線の傾き
n: ループ計算の回数
返り値:
価格と量のDataFrame
"""
p = p0 # 初期の価格
q_lst = []
p_lst = []
for i in range(n):
p = (a+c) / b - (d/b) * p
q = a - b * p
q_lst.append(q)
p_lst.append(p)
# 定常状態
pss = (a+c) / (b+d)
qss = a - b * pss
print(f'定常状態での価格:{pss:.1f}\n定常状態での量: {qss:.1f}')
dic = {'output':q_lst, 'price':p_lst}
return pd.DataFrame(dic)
まず\(\dfrac{d}{b}<1\)を仮定し収束するケースを考えよう。
cobweb(45, a=100, b=1.1, c=1, d=1, n=50).plot(secondary_y='price')
pass
定常状態での価格:48.1
定常状態での量: 47.1

コードの説明
.plot()の引数secondary_yは右の縦軸の変数をしている。ここでは'price'を指定している。凡例を見るとprice (right)となっている。
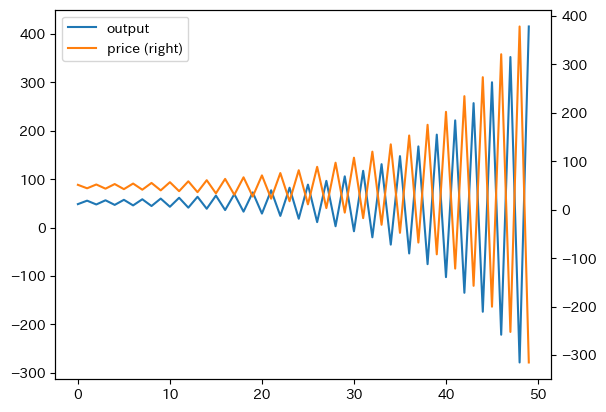
\(\dfrac{d}{b}>1\)を仮定し発散するケースをプロットする。
cobweb(45, a=100, b=1, c=1, d=1.1, n=50).plot(secondary_y='price')
pass
定常状態での価格:48.1
定常状態での量: 51.9