成長会計

in English or the language of your choice.

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import py4macro

# numpy v1の表示を使用
np.set_printoptions(legacy='1.21')
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")

はじめに

この章では次の問を考える。

（問２）なぜ国々の経済成長率は大きく異なるのか？

この問を成長会計と呼ばれる手法を使って考察する。この手法も発展会計と同様に，一人当たりGDPの変化率（即ち、経済成長率）を全要素生産性と蓄積生産要素に分解し、それぞれの寄与度を考察することにより問２の「なぜ」を考える。

成長率について

\(t\)時点の生産関数を

\[ y_t=A_tk_t^a\left(h_tH_t\right)^{1-a} \]

としよう。\(t\)時点と\(t+1\)時点の生産関数を使うと

\[ \frac{y_{t+1}}{y_t}=\frac{A_{t+1}}{A_t} \left(\frac{k_{t+1}}{k_t}\right)^a \left(\frac{h_{t+1}H_{t+1}}{h_tH_t}\right)^{1-a} \]

となる。ここで

\[ 1+g_x\equiv\frac{x_{t+1}}{x_t} \]

とすると，\(g_x\)は\(x\)の成長率（例えば、0.02）である。これにより、

\[ 1+g_y=(1+g_A)(1+g_k)^a\left[(1+g_h)(1+g_H)\right]^{1-a} \]

となり、対数化すると

\[ \log(1+g_y)=\log(1+g_A)+a\log(1+g_k)+(1-a)\left[\log(1+g_h)+\log(1+g_H)\right] \]

となる。また成長率が十分に小さい場合（例えば、0.02）、次式で近似することが可能となる。

(10)\[ \log(1+g_x)\approx g_x \]

np.log( 1+0.02 )

0.01980262729617973

即ち、

(11)\[ g_y=g_A+ag_k+(1-a)(g_h+g_H) \]

となる。

この式に基づき，成長会計，即ち，どの要素がどれだけ一人当たりGDPの成長率に貢献しているかを計算することになる。

次に変数の平均成長率の計算方法を説明する。ある変数\(x\)が毎年\(g_x\)の率（例えば，0.02）で\(n\)年間成長したとしよう。初期の\(x=x_0\)に対する\(n\)年後の比率を考えると，次式が成立する。

(12)\[ \frac{x_{n}}{x_{0}}= \frac{x_1}{x_{0}}\cdot \frac{x_2}{x_{1}}\cdot \frac{x_3}{x_{2}}\cdot \cdots \frac{x_{n-2}}{x_{n-3}}\cdot \frac{x_{n-1}}{x_{n-2}}\cdot \frac{x_n}{x_{n-1}} =(1+g_x)^{n} \]

\(g_x\)は一定なので\(g_x\)は年間平均成長率と等しい。このことを踏まえ(12)の両辺を\(1/n\)乗すると次式となる。

\[ \left(\frac{x_n}{x_0}\right)^{\frac{1}{n}}=1+g_x \]

即ち，\(1+g_x\)は\(\dfrac{x_n}{x_0}\)の幾何平均であり，平均成長率\(g_x\)はこの式を使い計算できる。

(13)\[ g_x= \left( \dfrac{x_{n}}{x_{0}} \right)^{\frac{1}{n}}-1 \]

この場合，算術平均ではなく幾何平均を使うことに注意しよう。また毎期毎期の成長率が違っても同じ結果(13)が成立することも覚えておこう。

更に，年間平均成長率を計算する場合，(12)の両辺を対数化し式(10)の近似を使うこともできる。

\[\begin{split} \begin{align*} \ln\left(\frac{x_n}{x_0}\right) &=\ln\left(1+g_x\right)^n \\ &\Downarrow \end{align*} \end{split}\]

(14)\[ g_x\approx\frac{1}{n}\ln\left(\frac{x_n}{x_0}\right) \]

\(g_x\)が十分に小さい場合は，(13)と(14)のどちらを使っても大きな差は出ない。重要な点は，どちらかの一つの方法を計算の対象全てに一貫して使うことであり，以下では(11)と(14)を使って計算する。

例：\(x_0=10\)，\(x_n=30\)，\(n=50\)

x0 = 10
xn = 30
n  = 50

houhou1 = ( xn / x0 )**(1/n) - 1
houhou2 = ( np.log(xn) - np.log(x0) ) / n

print(f'方法１：{houhou1:}\n方法２：{houhou2}')

方法１：0.022215413278477092
方法２：0.02197224577336219

コードの説明

• fは以前説明したf-stringである。houhou1とhouhou2にそれぞれの値を代入している。

• \nは改行を意味する。

平均成長率の計算

まずPenn World Tableを読み込み，国のリストを作成しよう

df = py4macro.data('pwt')

country_lst = df.loc[:,'country'].unique()

データに含まれる次の変数を使う。

• rgdpna：実質GDP

  • 経済成長を考える上で適している

• emp：雇用者数

• rkna：物的資本サービス

• hc：人的資本の指標

  • 教育年数と教育の収益から計算されている

以下で計算する変数とは次のように対応している。

• 一人当たりGDP：\(y_i\equiv\dfrac{Y_i}{L_i}=\) rgdpna/emp

• 一人当たり資本：\(k_i\equiv\dfrac{K_i}{L_i}=\) rkna/emp

• 労働者一人当たり人的資本サービス：\(h_iH_i=\) avhxhc

• 資本の所得シャア：\(\alpha=1/3\)（仮定）

• 蓄積生産要素：\(k_i^{\alpha}\left(h_iH_i\right)^{1-\alpha}\)

• 全要素生産性：\(A_i=\dfrac{y_i}{k_i^{\alpha}\left(h_iH_i\right)^{1-\alpha}}\)

それぞれの変数を計算しよう。

# 資本の所得シャア
a=1/3.0

# 一人当たりGDP
df['y'] = df['rgdpna'] / df['emp']

# 資本割合

df['k'] = df['rkna'] / df['emp']

# 蓄積生産要素
df['factors'] = df['k']**a * ( df['avh']*df['hc'] )**(1-a)

# 全要素生産性
df['tfp'] = df['y'] / df['factors']

これらの変数を使い，1999年から2019年の20年間のy、k、avh，hcの平均成長率を計算するが，まずそのための準備として関数を作成する。次のcalculate_growth関数は，country（国）のvar（変数）の平均成長率を返す。

def calculate_growth(country, var, start=1999, end=2019, df=df):

    """
    引数：
        country: 国名（文字列; 例えば，'Japan'）
        var: 変数名（文字列; 例えば，`y`）
    戻り値：
        `country`における`var`の平均成長率（浮動小数点型）
    """

    t = end - start                          #1

    cond1 = ( df.loc[:,'country']==country ) #2
    cond2 = ( df.loc[:,'year']==start )      #3
    cond3 = ( df.loc[:,'year']==end )        #4

    cond_start = ( cond1 & cond2 )           #5
    cond_end = ( cond1 & cond3 )             #6

    df_start = df.loc[cond_start,:]          #7
    df_end = df.loc[cond_end,:]              #8

    g = (1/t) * np.log( df_end[var].iloc[0] / df_start[var].iloc[0] ) #9
    
    return 100 * g   #10

コードの説明

• #1：何年間かを計算

• #2：国を選択する際の条件であり#5と#6で使う

• #3：最初の年を選択する際の条件であり#5で使う

• #5：最後の年を選択する際の条件であり``#6`で使う

• #6：最初の年と国を選択する際の条件であり#7でdf_startを作成する際に使う

• #7：最後の年と国を選択する際の条件であり#8でdf_endを作成する際に使う

• #8：最初の年のDataFrameを抽出

• #9：最後の年のDataFrameを抽出

• #10：平均成長率を計算する。

  • df_end[var]とdf_start[var]は列ラベルvarの列を抽出しており、Seriesとして返される。

  • .iloc[0]はSeriesの0番目の数値を取り出すメソッド

  • 成長率を計算しgに割り当てる。

• #11：％表示にして返す

例として，日本の一人当たりGDPの平均成長率を計算してみよう。

calculate_growth('Japan','y')

0.6956748904901194

次に，calculate_growth関数を使いいっきに全ての国の４つの変数の平均成長率を計算する。forループが二重（入れ子）になっている。

var_lst = ['y','k','avh','hc']   #1

growth_dic = {}             #2

for v in var_lst:           #3
    
    growth_lst = []         #4
    
    for c in country_lst:   #5
        
        g = calculate_growth(c, v)  #6
        
        growth_lst.append(g)        #7
            
    growth_dic[v] = growth_lst      #8

df_growth = pd.DataFrame({'country':country_lst,         #9
                          'y':growth_dic['y'],   #10
                          'k':growth_dic['k'],
                          'avh':growth_dic['avh'],
                          'hc':growth_dic['hc']})

コードの説明

• #1：成長率を計算する対象となる変数リスト

• #2：空の辞書。次の形になるように(1)の平均成長率のリストを格納する。

  • キー：変数名（y、k、hc）

  • 値：それぞれの国の成長率からなるリスト

• #3：var_lstに対してのforループ。１回目のループではyについて計算する。

• #4：空リスト（役割は以下で説明）

• #5：country_lstに対してのforループ。(3)の１回目のforループで変数yに対してcountry_lstにある国の成長率を下に続くコードを使って計算する。

• #6：calculate_growth関数を使い，国cの変数vの平均成長率を計算しgに割り当てる。

• #7：計算した成長率を(4)のリストに追加する。

• #8：ループが終わると、(4)のリストを(2)の辞書に追加する。

  • 辞書に追加する際に変数名vを指定することにより、次のペアのデータが追加される

    • キー：変数名（y、k、hc）

    • 値：それぞれの国の成長率のリスト

  • #3のforループの次の変数に移り、3.以下で説明した作業が繰り返される。

• #9：country_lstをDataFrameの列に設定

• #10：yの成長率をDataFrameの列に設定するが，その際，growth_dic['キー']でgrowth_dicのキーにあるリストを抽出している。

  • 下の３行はk，avh，hcに対して同じ作業を行なっている。

  • 新たに作成されるDataFrameは変数df_growthに割り当てられる。

df_growthの最初の５行を表示してみよう。

df_growth.head()

	country	y	k	avh	hc
0	Aruba	-0.157902	3.014877	NaN	NaN
1	Angola	2.119709	0.038051	NaN	0.732205
2	Anguilla	NaN	NaN	NaN	NaN
3	Albania	3.088791	4.265393	NaN	0.428109
4	United Arab Emirates	-2.160483	NaN	NaN	1.159700

Note

DataFrameにはグループ計算用のメソッドgroupbyが備わっており，それを使うとより短いコードでdf_growthを作成することができる。

def calc_growth(x):
    return (1/(len(x)-1))*np.log( x.iloc[-1] / x.iloc[0] )

cond1 = ( 1999 <= df['year'] )
cond2 = ( 2019 >= df['year'] )
cond = cond1 & cond2
df_growth = 100 * df.loc[cond,:].groupby('country')[['y','k','avh','hc']].agg(calc_growth)

ここを参考にしよう。

yの成長率のヒストグラムをプロットするが，ここではDataFrameのメソッドplot()を使う。まず使用する列を選んでメソッドplot()の引数にkind='hist'を指定するだけである。他の引数：

• bins=20：階級（棒）の数を指定する引数（デフォルトは10）

• edgecolor='white'：は棒の枠の色をしてする。ここでは白を使っている。

df_growth.plot.hist(y='y', bins=15, edgecolor='white')
pass

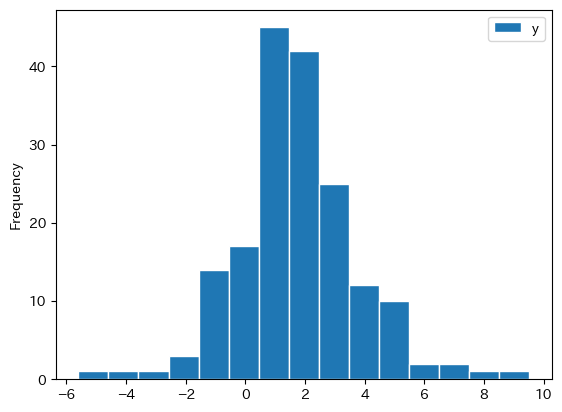
多くの国はプラスの経済成長を遂げているが，マイナイス成長の経済も存在する。平均成長率がマイナスの国数を計算してみよう。

cond = ( df_growth.loc[:,'y']<0 )
len(df_growth.loc[cond,:])

29

最も平均成長率が低い経済の国名を探してみよう。

df_growth_sorted = df_growth.sort_values('y')
df_growth_sorted.head()

	country	y	k	avh	hc
178	Venezuela (Bolivarian Republic of)	-5.346836	-1.519895	-0.286416	1.560305
181	Yemen	-4.512182	NaN	NaN	2.328553
130	Oman	-3.908885	-0.559118	NaN	NaN
4	United Arab Emirates	-2.160483	NaN	NaN	1.159700
94	Kuwait	-1.814703	2.198322	NaN	0.338220

ここで使ったメソッドsort_values()は，引数の列を基準に昇順に並べ替える。引数にascending=Falseを使うと，降順に並び替えることができる。

Show code cell source

Hide code cell source

print( '上のヒストグラムで最も成長率が低い国は'
      f'{df_growth_sorted.iloc[0,0]}である。')

上のヒストグラムで最も成長率が低い国はVenezuela (Bolivarian Republic of)である。

df_growth_sortedから分かるように，他の変数には欠損値が含まれているのでNaNがある行は全て削除する。

df_growth = df_growth.dropna().copy()

残った国数を確認してみよう。

len(df_growth)

63

蓄積生産要素の成長率

次に，下の式を使って蓄積生産要素の成長率を計算しよう。

\[ g_{\text{factors}}=ag_k+(1-a)(g_h+g_H) \]

結果をdf_growthに追加するが，その際、\(a=\dfrac{1}{3}\)と仮定する。

df_growth['factors'] = (
    (1/3) * df_growth['k'] +
    (1-1/3) * ( df_growth['avh'] + df_growth['hc'] )
)

factorsの成長率のヒストグラムを図示する。

df_growth.plot.hist(y='factors', bins=15, edgecolor='white')
pass

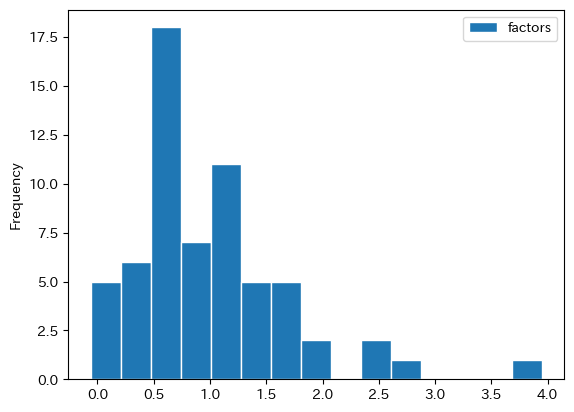
マイナスの成長率の国数を調べてみよう。

cond = ( df_growth.loc[:,'factors']<0 )
len(df_growth.loc[cond,:])

2

全要素生産性の成長率

全要素生産性は残差として計算される。

\[ g_A=g_y-g_{\text{factors}} \]

df_growth['tfp'] = df_growth['y'] - df_growth['factors']

tfpの成長率のヒストグラムを図示してみよう。

df_growth.plot.hist(y='tfp', bins=15, edgecolor='white')
pass

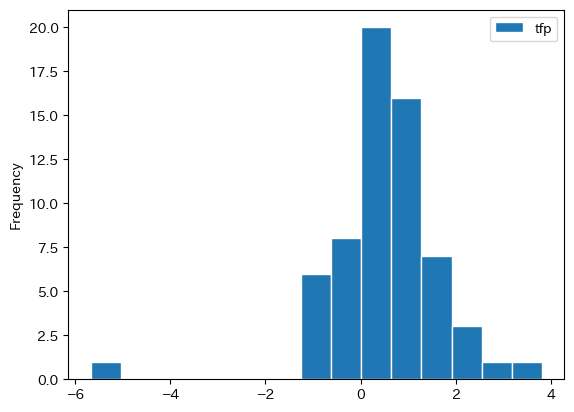
蓄積生産要素と比べると全要素生産性の成長率はよりマイナスに広がっている。TFP成長率がマイナスの国の数を確認してみよう。

cond = ( df_growth.loc[:,'tfp']<0 )
len(df_growth.loc[cond,:])

14

各国の全要素生産性の寄与度

全要素生産性と蓄積生産要素のどちらが成長率に貢献しているのだろうか。まず図を使って比較してみよう。

df_growth.plot.hist(y=['tfp','factors'], bins=20, alpha=0.5, edgecolor='white')
pass

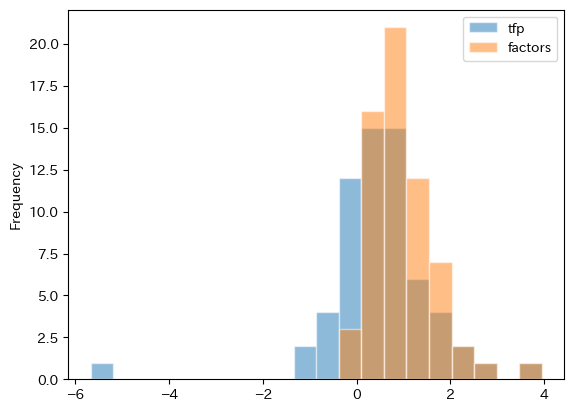
コードの説明

• ２つの列を選択することにより，同じ図に２つのヒストグラムが表示できるようになる。

• 引数alphaは図の透過度を指定する。0から1の間の値が指定可能で，デフォルトは1（透過なし）。

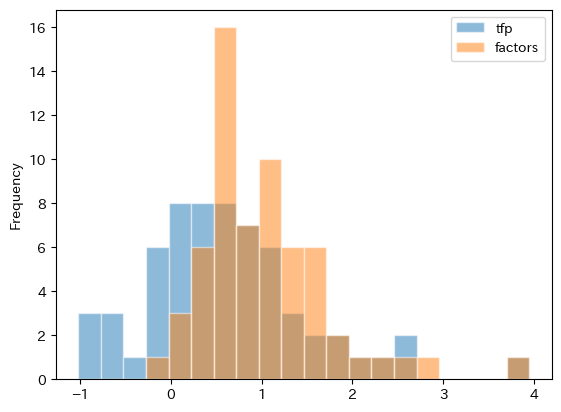
図から次のことがわかる。蓄積生産要素の成長率は正の値になる傾向がある。即ち，殆どの経済で蓄積生産要素による経済成長が起こっているということである。一方，全要素生産性の成長率はマイナスへの広がりがあり，成長を妨げる要因になっているようである。

次に，一人当たりGDPの成長率に対する全要素生産性の貢献度を数量化するが，まず，全要素生産性の成長率が一人当たりGDPの成長率の半分以上を占める国はデータセット全体の何％を占めるかを計算してみよう。

# tfpの成長率とyの成長率の比率
df_growth['tfp_y_ratio'] = 100 * df_growth['tfp'] / df_growth['y']

cond = ( df_growth.loc[:,'tfp_y_ratio']>=50 )
v = len(df_growth.loc[cond,:]) / len(df_growth)
print(f'全要素生産性の成長率が一人当たりGDPの成長率の半分以上を占める国の割合：{v:.1%}')

全要素生産性の成長率が一人当たりGDPの成長率の半分以上を占める国の割合：41.3%

コードの説明

f-stringを使って{v:.1%}のvの値を表示しているが，:.1%の部分は値を％表示にし小数点第一位まで表示することを指定している。

全要素生産性の重要性を示す結果と言って良いだろう。

一人当たりGDPの成長率に対する寄与度

発展会計で分散分解を使い，一人当たりGDPの成長率に対する全要素生産性と蓄積生産要素の寄与度を考える。 経済の成長率は次式で与えられる。

(15)\[ g_{y,i} = g_{A,i} + g_{\text{factors},i} \]

左辺の\(g_{y}\)の分散を次のように書き換えよう。 （分散と共分散のルールについてはここを参照しよう）。

(16)\[\begin{split} \begin{aligned} \text{Var}\left(g_{y,i}\right) &=\text{Cov}\left(g_{y,i},g_{y,i}\right)\\ &=\text{Cov}\left(g_{y,i},g_{A,i} + g_{\text{factors},i}\right)\\ &=\text{Cov}\left(g_{y,i},g_{A,i}\right)+\text{Cov}\left(g_{y,i},g_{\text{factors},i}\right) \end{aligned} \end{split}\]

＜計算の説明＞

• 1行目：変数が同じ場合の分散と共分散の関係を利用する。

• 2行目：式(15)を代入する。

• 3行目：\(g_{A,i} + g_{\text{factors},i}\)は線形となっているため，それぞれの共分散として展開することができる。

式(16)は一人当たりGDPの成長率の分散は全要素生産性と蓄積生産要素との共分散に分解できることを示している。 更に，両辺を\(\text{Var}\left(g_{y,i}\right)\)で割ると

\[ 1=\text{全要素生産性の寄与度}+\text{蓄積生産要素の寄与度} \]

となる。ここで、各寄与度は次のように定義される。

\[\begin{split} \begin{align*} \text{全要素生産性の寄与度}&= \dfrac{ \text{Cov}\left(g_{y,i},g_{A,i}\right) }{ \text{Var}\left(g_{y,i}\right) } \\ \text{蓄積生産要素の寄与度}&= \dfrac{ \text{Cov}\left(g_{y,i},g_{\text{factors},i}\right) }{ \text{Var}\left(g_{y,i}\right) } \end{align*} \end{split}\]

分母と分子にある分散と共分散を計算しよう。

cols = ['y', 'tfp', 'factors']
vcov = df_growth[cols].cov()
vcov

	y	tfp	factors
y	3.145373	2.116216	1.029157
tfp	2.116216	1.667260	0.448956
factors	1.029157	0.448956	0.580201

対角線にある値は各変数の分散となり，その他が各変数間の共分散となる。

# yの分散
y_growth_var = vcov.iloc[0,0]

# 共分散
y_tfp_growth_cov = vcov.iloc[0,1]
y_factors_growth_cov = vcov.iloc[0,2]

全要素生産性の寄与度

y_tfp_growth_cov / y_growth_var

0.6728028066006166

蓄積生産要素の寄与度

y_factors_growth_cov / y_growth_var

0.3271971933993832

蓄積生産要素と全要素生産性の寄与度は概ね6対4の割合でであることが確認できる。 即ち，一人当たりGDPの成長率の半分以上は全要素生産性に起因することを意味する。 この結果は両変数の成長率のヒストグラムからも伺える。 全要素生産性の方がより幅広く変化しているようである。 いずれにしろ，蓄積生産要素と全要素生産性ともに一人当たりGDPの成長に大きく貢献していることが確認できる。

表の作成

数カ国だけ取り出して表としてまとめてみよう。

country_table = ['Japan', 'United Kingdom','United States', 'Norway',
                'Singapore','Peru','India','China']

cond = df_growth['country'].isin(country_table)

col = ['country','y','factors','tfp','tfp_y_ratio']

df_growth.loc[cond,col].set_index('country') \
         .sort_values('y', ascending=False) \
         .round(2) \
         .rename(columns={'y':'一人当たりGDPの成長率(％)',
                          'factors':'蓄積生産要素の成長率(％)',
                          'tfp':'TFPの成長率(％)',
                          'tfp_y_ratio':'TFPの寄与度(％)'})

	一人当たりGDPの成長率(％)	蓄積生産要素の成長率(％)	TFPの成長率(％)	TFPの寄与度(％)
country
China	8.28	4.21	4.07	49.14
India	4.75	3.09	1.67	35.07
Peru	2.30	1.36	0.94	40.76
Singapore	1.81	1.06	0.74	41.17
United States	1.23	0.62	0.62	49.88
United Kingdom	0.86	0.65	0.20	23.83
Japan	0.70	0.38	0.32	45.58
Norway	0.61	0.83	-0.23	-37.35

右端の全要素生産性（TFP）の寄与度は，上で計算したtfp_y_ratioを使っており，一人当たりGDPの成長率のうち何％がTFPによるものかを示している。 この表から次の事が分かる。

• 全要素生産性の成長率が負の経済もあるため，TFPの寄与度が負になっている場合もある。その場合，蓄積生産要素の寄与度100％以上になる。

• 日本の全要素生産性の寄与度は非常に大きい。

このデータは1999~2019年のデータであり，それ以前ではどうだったのかを含めて，次節では年代を区切って日本の経済成長を考察してみることにする。

日本

日本の年代別に成長率を考えてみよう。まず次の関数を作成する。

def jp_growth_decomposition(start, end):
    """引数：
        start（int）: 開始年
        end（int）: 最終年
        
       返り値：次の変数の成長率とTFPの寄与度からなるリスト
                一人当たりGDP
                一人当たり物的資本
                平均労働時間
                人的資本
                全要素生産性（TFP）"""

    var_lst = ['y', 'k', 'avh', 'hc']
        
    g_lst = []
    
    # ========== var_listの変数の平均成長率を計算しg_listに追加する ==========
    for v in var_lst:
        
        g = calculate_growth(country='Japan', var=v, start=start, end=end)
        g_lst.append(g)
        
    # ========== 蓄積生産要素の平均成長率を計算しg_listに追加する ==========
    factors = (1/3) * g_lst[1] + (1-1/3) * ( g_lst[2]+g_lst[3] )
    g_lst.append(factors)
    
    # ========== 全要素生産性の平均成長率を計算しg_listに追加する ==========
    tfp = g_lst[0] - factors
    g_lst.append(tfp)

    # ========== 全要素生産性の寄与度を計算しg_listに追加する ==========
    tfp_contribution = 100 * tfp / g_lst[0]
    g_lst.append(tfp_contribution)
    
    return g_lst

この関数を使ってDataFrameを作成する。

dic = {}                                          # 1

yr_lst = ['1950s','1960s','1970s',                # 2
           '1980s','1990s','2000s','2010s']

for yr in yr_lst:                                 # 3
    start = int(yr[:4])                           # 4
    end = start+9                                 # 5
    dic[yr] = jp_growth_decomposition(start, end) # 6


idx = ['y_growth','k_growth',               # 7
       'avh_growth','hc_growth','factors_growth',
       'tfp_growth','tfp_contribution']

df_jp = pd.DataFrame(dic, index=idx)              # 8
df_jp

	1950s	1960s	1970s	1980s	1990s	2000s	2010s
y_growth	5.337782	7.701368	3.782054	3.864003	0.876690	0.524864	0.152147
k_growth	NaN	9.842525	8.042962	5.305180	4.224729	2.049854	0.183164
avh_growth	0.668055	-0.133175	-0.340549	-0.232066	-1.200796	-0.572358	-0.549697
hc_growth	1.257113	0.804446	0.708988	0.558892	0.515371	0.442203	0.302941
factors_growth	NaN	3.728356	2.926613	1.986277	0.951293	0.596515	-0.103449
tfp_growth	NaN	3.973013	0.855440	1.877726	-0.074603	-0.071651	0.255596
tfp_contribution	NaN	51.588399	22.618406	48.595346	-8.509593	-13.651379	167.992878

コードの説明

1~6のコードは次のコードをforループとして書いている。

dic = {'1950s':jp_growth_decomposition(1950,1959),
       '1960s':jp_growth_decomposition(1960,1969),
       '1970s':jp_growth_decomposition(1970,1979),
       '1980s':jp_growth_decomposition(1980,1989),
       '1990s':jp_growth_decomposition(1990,1999),
       '2000s':jp_growth_decomposition(2000,2010),
       '2010s':jp_growth_decomposition(2010,2019)}

1. 空の辞書dicを作成する。

2. dicのキーになる値のリストを作成する。

3. yr_lstに対してのforループ。

4. 関数jp_growth_decomposition()の引数として使用する開始年を作成する。

   • 右辺のyrは5つの文字からなる文字列であり，yr[:4]は最初の4文字を抽出する。それを整数に変換するためにint()を使っている。

   • 右辺の開始年を変数startに割り当てる。

5. 関数jp_growth_decomposition()の引数として使用する最終年を作成する。

   • 右辺ではstartの9年後を最終年としている。

   • 右辺の最終年を変数endに割り当てる。

6. dicのキーyrに対応する値としてjp_growth_decomposition(start,end)の返り値を`設定する。

7. (8)でDataFrameを作成するが，その行ラベルに使うリストを作成する。

8. dicを使いDataFrameを作成する。

値を確認するだけであればこのままでも良いが，棒グラフを作成するために列と行を入れ替えることにする。df_jpのメソッド.transpose()を使う。

df_jp = df_jp.transpose()
df_jp

	y_growth	k_growth	avh_growth	hc_growth	factors_growth	tfp_growth	tfp_contribution
1950s	5.337782	NaN	0.668055	1.257113	NaN	NaN	NaN
1960s	7.701368	9.842525	-0.133175	0.804446	3.728356	3.973013	51.588399
1970s	3.782054	8.042962	-0.340549	0.708988	2.926613	0.855440	22.618406
1980s	3.864003	5.305180	-0.232066	0.558892	1.986277	1.877726	48.595346
1990s	0.876690	4.224729	-1.200796	0.515371	0.951293	-0.074603	-8.509593
2000s	0.524864	2.049854	-0.572358	0.442203	0.596515	-0.071651	-13.651379
2010s	0.152147	0.183164	-0.549697	0.302941	-0.103449	0.255596	167.992878

1950年代に欠損値があるが，そのまま議論を進めよう。まず一人当たりGDP成長率gdp_pc_growthを棒グラフとして表示してみよう。表示したい列を選択し，引数にkind='bar'を選択するだけである。

df_jp.plot.bar(y='y_growth')
pass

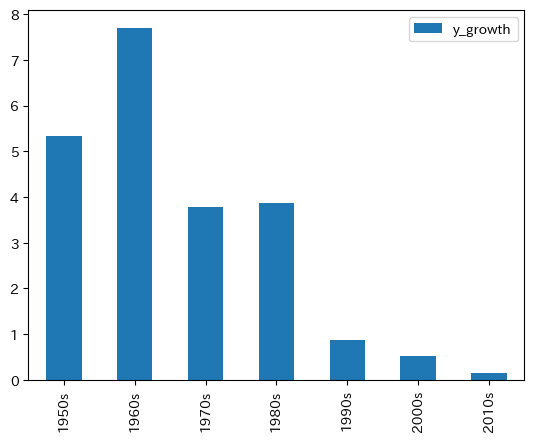
1960年代をピークに成長率は下降線をたどっている。

次にヒストグラムに異なる変数を並べて表示してみる。この場合も、表示したい変数を先に選びkind='bar'を指定するだけである。

cols = ['y_growth', 'factors_growth', 'tfp_growth']
df_jp.plot.bar(y=cols)
pass

以下では，全要素生産性と蓄積生産要素の成長率に焦点を当て議論を進めるためにdropna()を使って1950年代のデータは削除する。

df_jp = df_jp.dropna()

上の棒グラフで，引数stacked=Trueを設定すると棒を積み重ねて表示することができる。

df_jp.plot.bar(y=cols[1:], stacked=True)
pass

次のグラフでは，一人当たりGDPの線グラフと一緒に表示している。

ax_ = df_jp.plot(y=cols[0], marker='o',color='k', legend=True)
df_jp.plot.bar(y=cols[1:], stacked=True, legend=True, ax=ax_)
pass

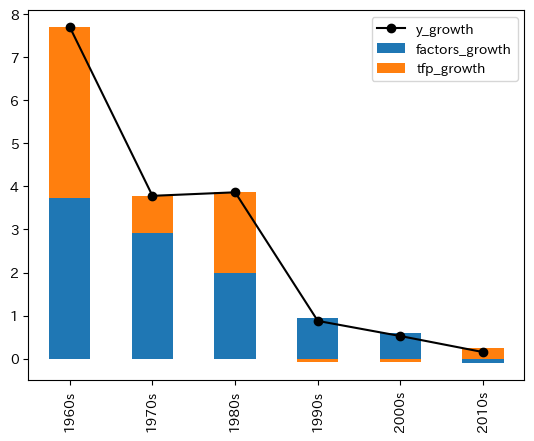
1990年代に入ると，それ以前と比べて全要素生産性の成長率の下落が著しく，一人当たりGDPの成長率に大きく影響している。「失われた10年」の原因と主張する研究者もいる。