定量的マクロ経済分析:Part 1#
import japanize_matplotlib
import numpy as np
import pandas as pd
import py4macro
import statsmodels.formula.api as smf
# numpy v1の表示を使用
np.set_printoptions(legacy='1.21')
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
はじめに#
本章と次章の目的は,回帰分析,差分方程式,ランダム変数を駆使し,定量(数量)的マクロ経済分析をおこなうことである。使うモデルは,中級レベルのマクロ経済学ではお馴染みの総需要・総供給モデル(ADASモデル)である。より具体的には,次の2ステップに分けて定量分析をおこなう。
景気循環に関するデータに基づきADASモデルのパラメーターの値を設定するカリブレーションと呼ばれる作業をおこなう。
ADASモデルの数量的な特徴を確認し,次の問いを検討する。
GDPと価格水準の長期トレンドからの乖離(%)の変動は,何パーセントが需要ショックにより引き起こされ,何パーセントが供給ショックに起因するのか?
本章では1について解説をおこない,次章で2について議論を展開する。
通常の教科書でのADASモデルを使う分析では,パラメータの符号(正か負)のみを仮定し,比較静学に基づきモデルの定性的な特徴や予測を考察する。例えば,政府支出の増加を考えてみよう。利子率は上昇し,短期的にはGDPも増加することになるが,「GDPの増加」は定性的な結果(予測)である。このような分析は経済を理解する上で有用な方法であるが,例えば,「GDPがどれだけ増加するのか」について答えることはできない。GDPの増分がどの程になるのかは,定量的な問題(予測)であり,総需要曲線と総供給曲線の傾き等の値を設定してこそ答えることができる問いである。
一方で,パラメータにランダムな値を使っても意味がある分析にはならない。そこで有用な手法がカリブレーションと呼ばれる分析方法である。詳細は以下で説明するが,簡単に言うと,カリブレーションではマクロ・データの特徴と整合的にパラメータの値を決定することになる。本章では,カリブレーションの考え方と中級+レベルで使えるツールを利用した方法を解説する。一旦,パラメータの値が決まるとより興味深い定量分析が可能となるが,次章で扱うことにする。
Note
ADASモデルの総需要曲線はISLMモデル(もしくは開放経済版であるマンデル=フレミング・モデル)から導出できる。即ち,ADASモデルの裏ではISLMモデルが動いているため,ADAS-ISLMと表現することもできる。一方で,殆どの大学院のマクロ経済学の授業ではADAS-ISLMモデルは学ばないのではないだろうか。その大きな理由は,合理的期待に基づく消費者・企業の最適化行動が明示的に反映されていないことである。その反動かもしれないが,ADAS-ISLMモデルは「初学者用」と思われる傾向がある。しかし実際には,政策を検討する際にADAS-ISLMモデルは参考にされている。内閣府は「経済環境の変化や財政金融政策が経済に与える影響を定量的に評価するため」に短期日本経済マクロ計量モデルを研究テーマとして挙げており,そこで展開されるのはADAS-ISLMモデルの開放経済版(マンデル=フレミング・モデル)である。もちろん,変数や式の数は比べものにならない程大掛かりなモデルとなっているが,基本的にはADAS-ISLMモデルである。
Hint
論文『経済マクロモデルについて ~その概要、歴史、シミュレーション等~』は,マクロ経済学において影響力があるモデルの歴史的な発展と現状について端的にわかり易く解説している。論文が掲載された「経済のプリズム」という雑誌は参議院事務局が編集・発行しており,政治家を主な読者としているためか,難しい数式は一切ない。興味がある人は是非読んでみよう。
ADASモデル#
ここでは総需要・総供給モデル(ADASモデル,Aggregate Demand and Aggregate Supply Model)の記号を整理し,景気循環データと整合性が保たれるように内生変数を解釈し直すことにより,定量分析の準備をおこなう。
モデルの構造#
短期総供給曲線(AS曲線)#
\(Y_t=\) 産出量の対数
\(Y_{*}=\) 自然産出量の対数
長期的なトレンドに対応する。
\(P_t=\) 物価水準の対数
\(P_t^e=\) \(P_t\)に対する予測値
\(v_t=\) 一過性の供給ショック
式(116)自体はAS曲線の典型的な式となっている。一方で,定量分析のために次の点に関して解釈し直している。
対数の役割:
内生変数である\(Y_t\)と\(P_t\)及び定数の\(Y_{*}\)は産出量と物価水準の対数としている。対数として解釈することにより,ADASモデルを使ってデータを捉えやすくする利点がある。また,より複雑な非線形のADASモデルを均衡周辺でテイラー近似した結果と解釈しても良いだろう。テイラー近似の手法は,研究で広く用いられる方法である。
供給ショックの種類:
一過性の総供給ショック\(v_t\)は長期的なトレンドから一時的な乖離を引き起こす要因となるものである。後に導入する物価水準の長期的トレンド\(P_{*}\)には影響を及ぼさないと仮定する。もちろん,供給ショックとなるため\(Y_{*}\)にも影響しない。
短期総需要曲線(AD曲線)#
\(u_t=\) 一過性の需要ショック
AD曲線はIS-LMモデルから導出することができるが,その場合,政府支出やマネーストックなど様々な変数に依存した複雑な式となる。式(117)は対数線形の簡単な式となっているが,その裏にあるのが次の考え方である。
政府支出や租税,マネーストック,更には,消費や投資水準は\(b\)及び\(u_t\)に含まれていると考える。また,それらの変化は全て需要ショックである\(u_t\)が捉えていると仮定する。
需要ショックには次の2つがあると仮定する。
需要ショック\(u_t\)は自然産出量水準\(Y_t^{*}\)には影響は与えないと仮定を置くとともに,ショック自体も永続的に維持されるのではなく,時間とともにフェードアウトする一過性のショックと仮定する。
このように簡略化することにより,景気循環データをADASモデルの枠組みの中で扱いやすくなる利点がある。
適応的期待#
適応的期待は「後ろ向き」の期待形成を仮定することになり,批判の的にもなり易い。しかし,最前線の研究でも取り上げられ,データの特徴を捉えた仮定と言えるだろう。
総需要・総供給ショック#
既に触れたが,一過性のショック項\(u_t\)と\(v_t\)は次の2点を満たすと仮定する。
物価水準トレンド\(P_{*}\)と自然産出量\(Y_{*}\)に影響を及ぼさない。
短期的・一時的なショックであり,永続的に正または負の一定の値を取り続けない。
一方で,確率的シミュレーションを行う際は,毎期毎期において一過性の総需要ショックと総供給ショックが発生する状況を考える。その場合,次のホワイト・ノイズの仮定を採用することになる。
Note
マクロ計量経済学の分野にベクトル自己回帰モデル(VAR, Vector Autoregression)と呼ばれる手法がある。その文献における「構造ショック」と\(u_t\)及び\(v_t\)がどう異なるかを考えてみよう。
VARモデルには構造型VARモデルと誘導型VARモデルの2つがあるが,ここで考えるのは前者である。その考え方を簡単に説明するために,例としてGDPと失業率の2変数のVARモデルを考えてみよう。構造型VARでは,\(t\)期のGDPは(i)\(t\)期の失業率,(ii)2変数の過去の値,(iii)\(t\)期のGDPショックの3つに依存すると考える。同様に,\(t\)期の失業率は同期のGDP,2変数の過去の値,そして失業率ショックに依存する。ここで重要になるのが次の点である。(ii)で使用する変数が十分に過去を遡った値(例えば,四半期データで\(t-1\)期から\(t-3\)期もしくは更に遡った値)であれば,(iii)のショックが次の3つの特徴を満たすということである。
均一分散
自己相関はない
GDPショックと失業率ショックは無相関
このようなショックを「構造ショック」と呼ぶ。なぜそう呼ばれるかを直感的に考えてみよう。経済メカニズムにより発生する変数の動きは,時間的なラグが存在したり(例えば,雇用の調整にはコストが掛かるが,それが非常に高い失業率の持続性の一つの要因と考えられる),他の変数の過去の値から影響を受けたりする(例えば,失業している間に労働者のスキルは失われ,それが将来のGDPに負の影響を及ぼす可能性がある)。このような経済メカニズムに起因する効果を捉えたのが(ii)の過去の変数である。2変数の時間的なラグが十分に長くなれば,殆どの経済メカニズムの効果は捉えることができるため,残っているのは(iii)にある経済メカニズムと無関係な純粋にランダムはショックということになる。それを「構造ショック」としてGDPショック,失業率ショックと呼んでいる。
ADASモデルの\(u_t\)と\(v_t\)はどうかというと,ADASモデルには十分な変数のラグが無いため上の「構造ショック」の3つの特徴を必ずしも満たすとは言えない。むしろ,\(u_t\)には\(p_t\)で捉えられていない政府,中央銀行,企業や消費者の\(y_t\)(\(Y_t\)のトレンドからの乖離)に対する影響を全て反映しており,ここではそれを総需要ショックと呼んでいる。同様に,\(v_t\)は適応的期待と\(y_t\)で捉えられていない,企業などの\(p_t\)(\(P_t\)のトレンドからの乖離)に対する影響を総需要ショックと呼んでいる。即ち,\(u_t\)と\(v_t\)には経済メカニズムにより発生するショックを含んでいると考えることができる。従って,\(u_t\)と\(v_t\)は,VARモデルでいう構造ショックとは異なることになる。
長期均衡とトレンドの決定#
長期均衡または定常状態(steady state)では次の条件が満たされることになる。
\(u_{t}=v_t=0\)
\(P_t=P_{t-1}=P_{*}\)
\(Y_t=Y_{*}\)
この場合AD曲線(117)は次の様になる。
この式は自然産出量と物価水準の長期的な関係を表している。 もちろん,トレンドのデータはある程度の変動を示しながら持続的に増加しており,式(119)は満たされない。 ここでは,数式を簡単にしつつデータと整合性がある様にするための単なる仮定であり,これにより以下で説明する式(120)と式(121)を簡単に導出することが可能となる。
一方で,自然産出量\(Y_{t*}\)と物価水準のトレンド\(P_{t*}\)が増加する改良バージョンを付録Aで展開している。 こちらの方がよりデータと整合的ではあるが,結局は,式(120)と式(121)が導出されることになる。 わざわざモデルを複雑にしなくても同じ均衡式が導出できるのであれば,簡単なバージョンで十分である。Simplicity is the best approach!
図示#
ADASモデルを図示するとFig. 9のようになる。長期均衡においてAD曲線とAS曲線は\(P_*\)と\(Y_*\)で交差することになる。短期均衡を考えるために,供給ショック\(v_t\)が1期間だけ正の値を取り,その後は0になるとしよう。ショックが発生するとAS曲線は上方シフトし,産出量は減少し物価水準は上昇する。適応的期待により,ショックがなくなってもAS曲線は直ぐには長期均衡に戻らず,徐々に下方シフトすることになり,最終的には長期均衡に経済は戻ることになる。
このような分析は,教科書で解説される典型的な例である。長期均衡は安定的であり,産出量と物価水準は少しずつ動くという結果は直観的であり分かり易い。しかし,このような定性的な分析からは,ショック発生後に経済はどれだけの時間をかけて長期均衡に戻るかについては何もわからない。また,長期均衡に戻るスピードが何に依存しているのかも分からない。AD曲線とAS曲線の傾きが影響を及ぼしそうだと想像できるが,傾きが急だと戻るスピードが早いのだろうか,遅いのだろうか。このような問は,定量分析をおこなうことにより簡単に確認することが可能となる。
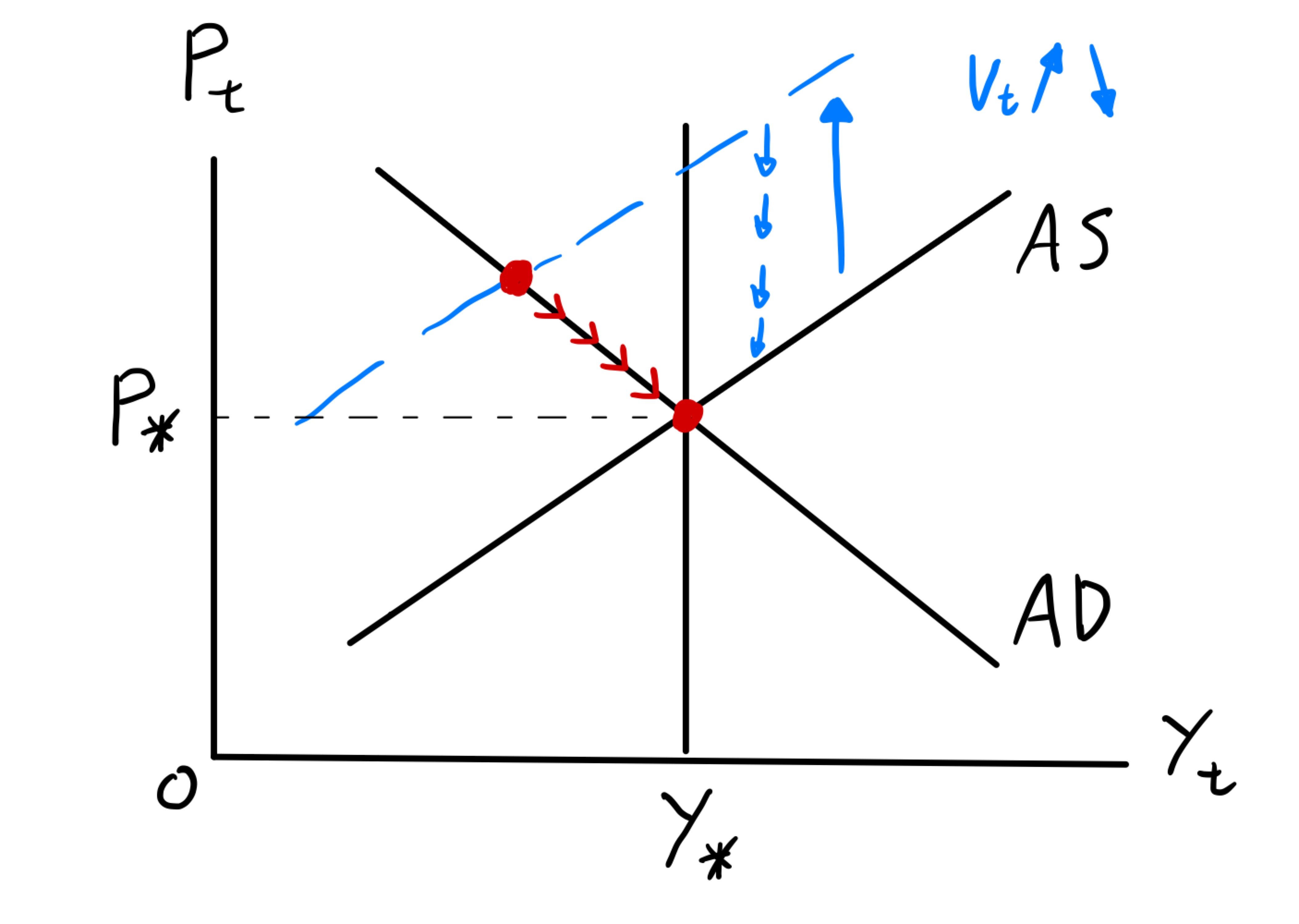
Fig. 9 産出量と物価水準で表したADASモデル#
均衡式#
ADASモデルとデータの親和正を高めるために次の変数を定義しよう。
\(p_t=P_t-P_{*}\):価格水準のトレンドからの乖離率
\(y_t=Y_t-Y_{*}\):産出量のトレンドからの乖離率
\(p_t\)と\(y_t\)を使ってAS曲線とAD曲線を書き換えることにする。
AS曲線#
この式はAS曲線を産出量と物価水準のトレンドからの乖離率で表している。また,この式から供給ショック\(v_t\)について次のことが言える。
直接効果:\(p_{t-1}\)と\(y_t\)を所与とすると,\(v_t\)の1単位上昇は物価水準のトレンドからの乖離を1%発生させる。
間接効果:\(p_{t}\)と\(y_t\)は均衡で決定されるため,\(v_t\)が変化すると\(y_t\)も変化し,その効果を通して\(p_{t}\)が変化する。
直接効果と間接効果の相互作用により供給ショック\(v_t\)は\(p_t\)に影響を及ぼすことになる。
AD曲線#
式(117)の両辺から式(119)を引くと次の1行目となる。
この式はAS曲線を産出量と物価水準のトレンドからの乖離率で表している。また,この式から供給ショック\(v_t\)について次のことが言える。
この式はAD曲線を産出量と物価水準のトレンドからの乖離率で表している。また,この式から需要ショック\(u_t\)について次のことが言える。
直接効果:\(p_{t}\)を所与とすると,\(u_t\)の1単位上昇は産出量のトレンドからの乖離を1%発生させる。
間接効果:\(p_{t}\)と\(y_t\)は均衡で決定されるため,\(u_t\)が変化すると\(p_t\)も変化し,その効果を通して\(y_{t}\)が変化する。
直接効果と間接効果の相互作用により供給ショック\(u_t\)は\(y_t\)に影響を及ぼすことになる。
長期均衡#
長期均衡または定常状態(steady state)では次の条件が満たされることになる。
\(u_{t}=v_t=0\):ショックはない
\(p_* =0\):トレンドからの乖離率はゼロ
\(y_* =0\):トレンドからの乖離率はゼロ
図示#
ADASモデルを乖離率の変数\(p_t\)と\(y_t\)で表した図がFig. 10である。原点が長期均衡となる。Fig. 9と同じように,総供給ショック\(v_t\)が1期間だけ正の値を取り,その後は0になる場合を考えてみよう。ショックが発生するとAS曲線は上方シフトし,産出量の乖離率は負の値となるが,物価水準の乖離率は正の値を取ることになる。ショックが0に戻った後,AS曲線は徐々に下方シフトし,最終的には長期均衡(原点)に経済は戻ることになる。以下の分析では,乖離率の変数である\(p_t\)と\(y_t\)を使うが,Fig. 10を念頭に置き結果を解釈するとわかり易いだろう。
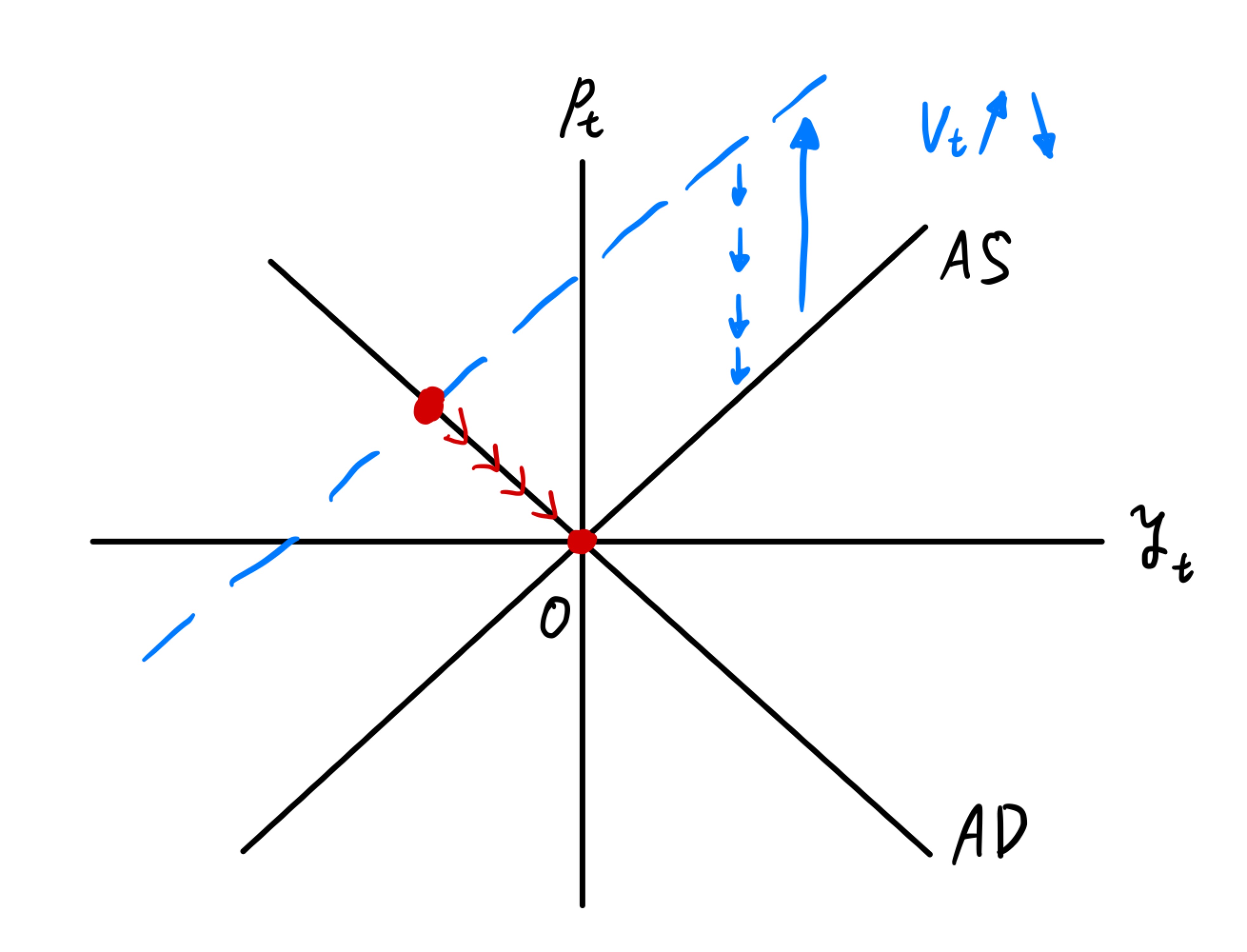
Fig. 10 産出量と物価水準のトレンドからの乖離率で表したADASモデル#
景気循環のデータ#
トレンドからの乖離率#
ここでは式(120)と式(121)を使い定量分析をおこなうが,まず,それらの式と整合性があるデータの特徴を考える。\(y_t\)と\(p_t\)はトレンドからの乖離率となるため,py4macroのtrend()関数を使い,対応する変数を作成することにする。
df = py4macro.data('jpn-q')
df.columns
Index(['gdp', 'consumption', 'investment', 'government', 'exports', 'imports',
'capital', 'employed', 'unemployed', 'unemployment_rate', 'hours',
'total_hours', 'inflation', 'price', 'deflator'],
dtype='object')
\(Y_t\)にはgdpを使い,\(P_t\)にはdeflatorを使うことにする。
次のコードで作成するgdp_cycleとdeflator_cycleは,0を中心に上下する系列となる。
for c in ['gdp','deflator']:
df[c+'_cycle'] = np.log(df[c]) - py4macro.trend( np.log(df[c]) )
df.head()
| gdp | consumption | investment | government | exports | imports | capital | employed | unemployed | unemployment_rate | hours | total_hours | inflation | price | deflator | gdp_cycle | deflator_cycle | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1980-01-01 | 269747.5 | 153290.7 | 65029.2 | 73039.5 | 18383.8 | 24278.8 | 833041.425949 | 5506.000000 | 107.666667 | 1.900000 | 124.7 | 686598.200000 | 5.766667 | 71.011939 | 91.2 | 0.003269 | -0.025798 |
| 1980-04-01 | 268521.8 | 153551.9 | 65316.6 | 72164.5 | 18631.4 | 25454.5 | 843748.581006 | 5525.666667 | 110.000000 | 1.966667 | 124.8 | 689603.200000 | 8.166667 | 72.917251 | 93.4 | -0.010845 | -0.006555 |
| 1980-07-01 | 274183.1 | 155580.0 | 65765.9 | 72663.8 | 18449.3 | 23885.7 | 855449.381902 | 5561.333333 | 116.000000 | 2.033333 | 124.0 | 689605.333333 | 8.200000 | 73.897654 | 94.4 | 0.000457 | -0.000482 |
| 1980-10-01 | 279601.8 | 156162.4 | 66017.5 | 74761.1 | 19705.4 | 23716.5 | 867991.306098 | 5551.333333 | 123.333333 | 2.166667 | 124.0 | 688365.333333 | 8.100000 | 74.767147 | 95.4 | 0.010468 | 0.005515 |
| 1981-01-01 | 281995.7 | 156757.7 | 66259.0 | 76127.6 | 20289.5 | 24174.1 | 878387.487376 | 5568.666667 | 124.333333 | 2.200000 | 123.6 | 688287.200000 | 6.833333 | 75.690241 | 95.6 | 0.009441 | 0.003126 |
gdp_cycleとdeflator_cycleをプロットし,データのイメージを掴んでおこう。
ax_ = df.plot(y=['gdp_cycle','deflator_cycle'])
ax_.axhline(0, color='red')
pass
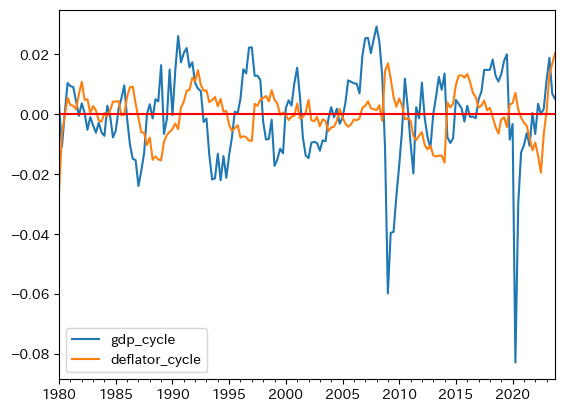
以下では,gdp_cycleとdeflator_cycleの3つの特徴に焦点を当て議論を進めることにする。
データの特徴1#
y_std = df.loc[:,'gdp_cycle'].std()
p_std = df.loc[:,'deflator_cycle'].std()
print(f'GDPのトレンドからの乖離率の標準偏差:{y_std:.6f}')
print(f'デフレータのトレンドからの乖離率の標準偏差:{p_std:.6f}')
# 不偏分散の平方根
GDPのトレンドからの乖離率の標準偏差:0.014833
デフレータのトレンドからの乖離率の標準偏差:0.007490
2つの数値を比べると,GDPの乖離率の標準偏差はデフレーターの約2倍あることが分かる。これは上のプロットでgdp_cycleの変動幅が大きいことを反映している。
データの特徴2#
y_autocorr = df.loc[:,'gdp_cycle'].autocorr()
p_autocorr = df.loc[:,'deflator_cycle'].autocorr()
print(f'GDPのトレンドからの乖離率の自己相関係数:{y_autocorr:.3f}')
print(f'デフレータのトレンドからの乖離率の自己相関係数:{p_autocorr:.3f}')
GDPのトレンドからの乖離率の自己相関係数:0.697
デフレータのトレンドからの乖離率の自己相関係数:0.830
失業やインフレ率などのマクロの変数は、前期の値が高ければ(低ければ)今期も高い(低い)傾向にあるが、この特徴を持続性(persistence; 慣性とも訳される)と呼ぶ。自己相関係数は持続性をとらえており、上の数値はデフレータの方がより高い持続性があることを意味する。
データの特徴3#
yp_corr = df.loc[:,['gdp_cycle', 'deflator_cycle']].corr().iloc[0,1]
print(f'GDPとデフレータの乖離率の相関係数:{yp_corr:.3f}')
GDPとデフレータの乖離率の相関係数:-0.153
この値は同じ期の相関係数であり,絶対値は小さく弱い関係にある。しかし,直感的にはgdp_cycleとdeflator_cycleの正の相関をイメージするのではないだろうか。正のGDPの乖離率は景気が良いことを示しているため,物価水準であるデフレーターもトレンドから正の方向に乖離するのではないか,という考えである。そのような考え方は基本的には正しいと言えるだろう。ただ,データを見る限り時間のズレがあるようだ。プロットを見ると,正の方向にGDPの乖離率が発生した後にデフレーターの正の乖離が発生しているように見える。次のプロットは,\(t\)期のgdp_cycleと\(t+\)6期のdeflator_cycleを重ねて図示している。同じ方向に動いていることを示しているとともに,相関係数も約0.433となっており,正の相関を数値でも確認できる。一つの可能性として次の解釈が成り立つ。デフレーターの変化には時間がかかり,それは価格の粘着性の反映かもしれない。
t_shift = 6
tmp = df.copy()
tmp['deflator_cycle_shift'] = tmp['deflator_cycle'].shift(-t_shift)
ax_ = tmp.plot(y=['gdp_cycle', 'deflator_cycle_shift'])
ax_.axhline(0, color='red')
yp_corr_shift = tmp[['gdp_cycle', 'deflator_cycle_shift']].corr().iloc[0,1]
print(f'GDPと{t_shift}期先のデフレータの乖離率の相関係数:{yp_corr_shift:.3f}')
GDPと6期先のデフレータの乖離率の相関係数:0.433
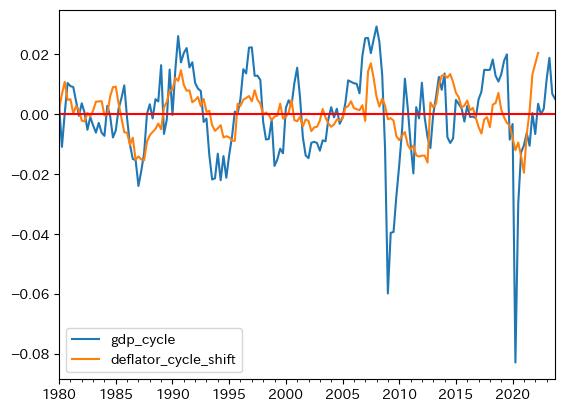
これらのデータの特徴1〜3をどこまで再現できるかに基づいてADASモデルを評価することになる。
カリブレーション#
はじめに#
定量分析を進めるためには,ADASモデルのパラメータに値を設定する必要がある。 ここでは景気循環のデータに基づき,次の4つのパラメーターの値を決めていく
\(a\) (AS曲線の傾き)
\(c\) (AD曲線の傾き)
\(\sigma_v\) (供給ショックの標準偏差)
\(\sigma_u\) (需要ショックの標準偏差)
パラメーターの値の決め方には主に次の2つある。
データに基づいて計量経済学的な手法などを用いて推定した結果を使う。
既存の実証研究で報告され推定値を使う。
多くの研究の場合,これらの方法を駆使して値を決めることになる。 また,必ずしも対象の経済モデルに基づいた推定結果でなくとも構わない。 以下では1番目の方法を使い議論を進めることにする。
カリブレーションとは#
2つの体重計があるとしよう。 一つは,市販の正確な体重計で誤差はない。 もう一つは自作の体重計で,作ったばかりなので精度に欠ける。 自作体重計にはスイッチが取り付けられており,それを調整することにより誤差を小さくし精度を高めることができる。 そのスイッチの使い方は次のようになる。 まず市販の体重計で自分の体重を測る。 次に自作体重計で測り同じ数値が出るようにスイッチを調整する。 このように,基準となる機器に基づいて測定器の誤差をなくすための調整をおこなうことをカリブレーションと呼ぶ。 自分の体重を使ってカリブレーションをおこない,親族や友達が使っても体重を正確に測れる場合は,手作り体重計の成功ということである。 一方で,自分以外の体重を測ると誤差が残る場合は,手作り体重計は100%成功とは言えないだろう。 60kg以上の体重は誤差が大きいが,60kg未満であればある程度の精度が確保できている場合はどうだろうか。 「60kg未満の体重を測る」が目的である場合,手作り体重計の成功と考えることもできるだろう。
このカリブレーションという手法は,最近のマクロ経済学の研究で広く使われており,その分野を定量的(数量的)マクロ経済学と呼ぶ。 ここではAD-ASモデルに応用しようというのが目的である。 体重計の例を使うと,AD-ASモデルと実際経済の関係は次のようになる。
市販の正確な体重計 → 日本経済
手作り体重計 → ADASモデル
手作り体重計のスイッチ → ADASモデルのパラメーター(外生変数)
スイッチの調整 → パラメーターの値の設定
カリブレーションで使うデータ
自分の体重 → 景気循環に関する特徴
評価方法
他の人の体重を測り手作り体重計の誤差を確認 → ADASモデルのパラメーターの設定に使われていないデータをどれだけ説明できるかの確認
均衡式の整理#
カリブレーションでは,パラメータaとcを推定する必要があるが,上の式を回帰式として使うには同時性の問題がある。
式(122)を\(\Delta p_{t}=ay_{t}+v_{t}\),\(\Delta p_{t}\equiv p_{t}-p_{t-1}\)に変形して回帰式として解釈し,\(a\)を推定することが考えられる。しかし,供給ショック\(v_t\)は\(p_t\)に影響を与え,式(123)を通して\(y_t\)にも影響を及ぼすことが考えられる。即ち,\(v_t\)と\(y_t\)が相関し,このままでは\(a\)の推定値は不偏性も一致性も失うことになる。また,式(123)をそのまま回帰式として解釈し,\(c\)を推定しても類似の問題が考えられる。
この点を回避するために,式(121)を式(120)に代入し次のように整理する。
ここで
また,式(124)を(123)に代入し,hの定義を利用し整理すると次式となる。
この結果を利用すると,ADASモデルを次の2つの式で表すことができる。
準備:\(h\)の推定値#
式(126)を回帰式と捉えて,まずは\(h\)の推定値を計算する。
まず,dfのメソッド.shift()を使ってdeflator_cycleを1期ずらした列をdeflator_cycle_lagとしてdfに追加しよう。
df['deflator_cycle_lag'] = df['deflator_cycle'].shift()
df.iloc[:5,-4:]
| deflator | gdp_cycle | deflator_cycle | deflator_cycle_lag | |
|---|---|---|---|---|
| 1980-01-01 | 91.2 | 0.003269 | -0.025798 | NaN |
| 1980-04-01 | 93.4 | -0.010845 | -0.006555 | -0.025798 |
| 1980-07-01 | 94.4 | 0.000457 | -0.000482 | -0.006555 |
| 1980-10-01 | 95.4 | 0.010468 | 0.005515 | -0.000482 |
| 1981-01-01 | 95.6 | 0.009441 | 0.003126 | 0.005515 |
deflator_cycle_lagには1期前のdeflator_cycleの値が,d_deflator_cycleには前期との差分が並んでいるのが確認できる。
まず回帰分析をおこない,その結果を表示する。
res_h = smf.ols('deflator_cycle ~ deflator_cycle_lag', data=df).fit()
print(res_h.summary())
OLS Regression Results
==============================================================================
Dep. Variable: deflator_cycle R-squared: 0.689
Model: OLS Adj. R-squared: 0.688
Method: Least Squares F-statistic: 384.1
Date: Wed, 11 Feb 2026 Prob (F-statistic): 8.56e-46
Time: 10:32:14 Log-Likelihood: 716.66
No. Observations: 175 AIC: -1429.
Df Residuals: 173 BIC: -1423.
Df Model: 1
Covariance Type: nonrobust
======================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept 0.0002 0.000 0.795 0.428 -0.000 0.001
deflator_cycle_lag 0.8194 0.042 19.597 0.000 0.737 0.902
==============================================================================
Omnibus: 48.339 Durbin-Watson: 1.616
Prob(Omnibus): 0.000 Jarque-Bera (JB): 109.483
Skew: 1.218 Prob(JB): 1.68e-24
Kurtosis: 6.014 Cond. No. 136.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
<推定結果について>
残差の自己相関を考えてみよう。ダービン・ワトソン検定統計量は1.616であり,「不明」の領域にある。しかし,付録BではBreusch-Godfrey検定とLjung-Box検定をおこなっているが,帰無仮説である「残差の自己相関なし」は棄却されてしまう。この結果により,説明変数deflator_cycle_lagと誤差項の相関の疑いがあり,hの推定値は不偏性も一致性も満たさないことになってしまう。この問題を解決するために,一般化最小二乗法の一つであるコクラン=オーカット推定法(Cochrane-Orcutt推定方)を使い推定をおこなうことにする。残差はAR(1)と置いて推定を進める。
\(1<\rho_p<1\)
\(\eta_t\)はホワイト・ノイズ
コードは簡単で,statsmodelsの.ols()関数の代わりに.glsar()関数を使う(glsarはGeneralized Linear Squares with Autoregressive Errorsの略)。ただ,次の点が異なる。
引数は
.ols()関数と似ている。第一引数:文字列の推定式(
.ols()と同じ)第二引数(
data):データの指定(.ols()と同じ)第三引数(
rho=1):n次自己回帰過程のnを指定(デフォルトは1)
未知の自己相関係数を計算する反復推定をおこなうために,
.fit()の代わりに次の引数を使いiterative_fit()を使用する。itermax=3:反復計算を最大回数(デフォルトは3)。cov_type='HC1'(オプショナル):不均一分散頑健推定を指定(不均一分散頑健推定についてはPythonで学ぶ入門計量経済学ー不均一分散を参照しよう)
res_h_glsar = smf.glsar('deflator_cycle ~ deflator_cycle_lag', # 推定式
data=df, # データの指定
rho=1 # AR(1)を指定
).iterative_fit(itermax=10, # 最大反復計算回数
cov_type='HC1' # 不均一分散頑健推定
)
print(res_h_glsar.summary())
GLSAR Regression Results
==============================================================================
Dep. Variable: deflator_cycle R-squared: 0.641
Model: GLSAR Adj. R-squared: 0.639
Method: Least Squares F-statistic: 175.0
Date: Wed, 11 Feb 2026 Prob (F-statistic): 5.17e-28
Time: 10:32:14 Log-Likelihood: 720.75
No. Observations: 174 AIC: -1438.
Df Residuals: 172 BIC: -1431.
Df Model: 1
Covariance Type: HC1
======================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept 0.0002 0.000 0.448 0.654 -0.001 0.001
deflator_cycle_lag 0.8188 0.062 13.230 0.000 0.697 0.940
==============================================================================
Omnibus: 53.697 Durbin-Watson: 2.037
Prob(Omnibus): 0.000 Jarque-Bera (JB): 151.719
Skew: 1.257 Prob(JB): 1.13e-33
Kurtosis: 6.822 Cond. No. 137.
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity robust (HC1)
hの推定値は大きく変わらないが,残差の系列相関はそれ程大きくないためだ。統計的優位性も高く,コクラン=オーカット推定法による式の変形後の残差の系列相関も排除できる。またこの計算では,不均一分散の可能性も排除できないため,不均一分散頑健推定も使っており,\(t\)検定は有効と考えることができる。ここで計算した値をhの推定値として採用し変数hhatに割り当てることにする。
また以下の分析では残差も必要になるが,コクラン=オーカット推定法で計算した\(\hat{e}_{pt}\)を変数epに割り当てることにする。
ep = res_h_glsar.resid
Note
反復計算をする度に係数の推定値と\(\hat{\rho}_p\)の値は変化するが
res_h_glsar.history
を使うと確認することができる。式(128)の自己相関係数\(\hat{\rho}_p\)の推定値にアクセスするには次のコードを使うと良いだろう。
res_h_glsar.model.rho
また,残差\(e_{pt}\)は
res_h_glsar.resid
で,また\(\eta_t\)は
res_h_glsar.wresid
で抽出できる。
最初のスイッチ:\(c\)の値#
ここではhhatを利用してcの推定値を計算するために,式(127)を回帰式として使う。
式(127)を再掲しよう。
\(d\equiv -ch\)
\(e_{yt}\equiv hu_t-chv_t\)
説明変数である\(p_{t-1}\)は誤差項\(e_{yt}\)とは期間がズレているため,残差に系列相関がなければ推定値は一致性を満たすことになる(不偏性は満たさない)。
res_d = smf.ols('gdp_cycle ~ deflator_cycle_lag', data=df).fit()
print(res_d.summary())
OLS Regression Results
==============================================================================
Dep. Variable: gdp_cycle R-squared: 0.041
Model: OLS Adj. R-squared: 0.035
Method: Least Squares F-statistic: 7.398
Date: Wed, 11 Feb 2026 Prob (F-statistic): 0.00719
Time: 10:32:14 Log-Likelihood: 492.28
No. Observations: 175 AIC: -980.6
Df Residuals: 173 BIC: -974.2
Df Model: 1
Covariance Type: nonrobust
======================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept -6.676e-05 0.001 -0.060 0.952 -0.002 0.002
deflator_cycle_lag -0.4099 0.151 -2.720 0.007 -0.707 -0.112
==============================================================================
Omnibus: 58.282 Durbin-Watson: 0.633
Prob(Omnibus): 0.000 Jarque-Bera (JB): 236.393
Skew: -1.212 Prob(JB): 4.66e-52
Kurtosis: 8.152 Cond. No. 136.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
<推定結果について>
\(d\)の推定値である\(\hat{d}\)は負であり,モデルに沿った結果である。
しかし,Durbin-Watson検定統計量は0.633であり残差の正の系列相関が強く疑われる。
従って,deflator_cycle_lagと残差の相関の可能性があり,推定値の一致性が失われている可能性が高い。
この問題に対処するために,hの推定値を計算した時と同じように,コクラン=オーカット推定法を使い推定をおこなう。
結果は次の通りである。
res_d_glsar = smf.glsar('gdp_cycle ~ deflator_cycle_lag', data=df).iterative_fit(10, cov_type='HC1')
print(res_d_glsar.summary())
GLSAR Regression Results
==============================================================================
Dep. Variable: gdp_cycle R-squared: 0.007
Model: GLSAR Adj. R-squared: 0.001
Method: Least Squares F-statistic: 0.5500
Date: Wed, 11 Feb 2026 Prob (F-statistic): 0.459
Time: 10:32:14 Log-Likelihood: 544.68
No. Observations: 174 AIC: -1085.
Df Residuals: 172 BIC: -1079.
Df Model: 1
Covariance Type: HC1
======================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept 0.0004 0.003 0.147 0.883 -0.005 0.005
deflator_cycle_lag -0.2202 0.297 -0.742 0.458 -0.802 0.362
==============================================================================
Omnibus: 151.661 Durbin-Watson: 2.052
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3130.415
Skew: -3.044 Prob(JB): 0.00
Kurtosis: 22.867 Cond. No. 75.8
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity robust (HC1)
dの推定値は絶対値で大きく減少しており,系列相関の影響が大きいことを示している。
不均一分散の可能性も排除できないため,不均一分散頑健推定を使っているが,残念ながら統計的優位性は低い。
この値をdの推定値として変数dhatに使うことにする。
dの推定値が確定した訳だが,\(-d\equiv ch\)で与えられ,\(c\)の推定値を次式で計算することができる。
この値をchatに割り当てよう。
chat = -dhat / hhat
chat
0.26898029722245514
これが「最初のスイッチの調整」である。
また以下の分析では残差も必要になるため,コクラン=オーカット推定法で計算した\(\hat{e}_{yt}\)を変数epに割り当てることにする。
ey = res_d.resid
2つ目のスイッチ:\(a\)の値#
式(125)では,\(h\)は\(a\)と\(c\)の関数となっている。 すでに\(h\)と\(c\)の推定値を計算しているため,この式を使うことにより簡単に\(a\)の推定値を計算することができる。 式(125)を整理すると次式となる。
計算結果をahatに割り当てよう。
ahat = (1/hhat - 1) / chat
ahat
0.8227478597716609
これが「2つ目のスイッチの調整」である。
3つ目のスイッチ:\(\sigma_v\)の値#
\(\sigma_v^2\)の値も回帰式の結果を使い設定する。 式(126)の誤差項\(e_{pt}\)は\(u_t\)と\(v_t\)の線形関数となっており,同様に,式(127)の誤差項\(e_{yt}\)も\(u_t\)と\(v_t\)の線形関数となっている。 以下に再掲する。
これはAD-ASモデルを前提とした理論上の関係であり,全てが観測不可能である。 しかし,\(a\)と\(h\)にはその推定値\(\hat{a}\)と\(\hat{h}\)を使い,\(e_{pt}\)と\(e_{yt}\)については残差\(\hat{e}_{pt}\)と\(e_{yt}\)を用いることにより,\(u_t\)と\(v_t\)を求めることが可能である。 式(130)は\(u_t\)と\(v_t\)の線形連立方程式となっているため,簡単に次のように書き直すことができる。
ここで\(\hat{e}_{pt}\)と\(\hat{e}_{yt}\)は残差を,\(\hat{a}\)と\(\hat{c}\)は推定値を表しており,これらを使って計算した需要・供給ショックを\(\hat{v}_t\)と\(\hat{u}_t\)として表している。
まず式(131)を使い,結果をvtに割り当てよう。
vt = ep - ahat*ey
vtのデータ型はSeriesであり,メソッド.std()を使うと簡単にvtの標準偏差を計算することができる。
結果をv_stdに割り当てよう。
v_std = vt.std()
v_std
0.01254675097212466
この値を\(\sigma_v\)に使うことにする。これが「3つ目のスイッチの調整」である。
4つ目のスイッチ:\(\sigma_u\)の値#
同様に,式(132)を使うと,\(\hat{u}_t\)の標準偏差を計算することができる。
u_stdに割り当てる。
ut = ey + chat*ep
u_std = ut.std()
u_std
0.014633934415444881
この値を\(\sigma_u\)に使うが,これが「最後のスイッチの調整」となる。
パラメーターの値:再掲#
print(f'aの値:{ahat:.3f}')
print(f'cの値:{chat:.3f}')
print(f'vの標準偏差:{v_std:.6f}')
print(f'uの標準偏差:{u_std:.6f}')
aの値:0.823
cの値:0.269
vの標準偏差:0.012547
uの標準偏差:0.014634
v_stdとu_stdを比べると,後者の値が若干大きい様である。
比率を計算してみよう。
u_std / v_std
1.166352504162819
ショックの直接的な影響だけを考えると,比較的にAD曲線の変動幅が大きいことを示している。 次章では,これらの値を使い定量分析を更に進めていく。
付録#
付録A#
この付録は次の2点を示すことを目的としている。
拡張モデル#
物価水準のトレンドの式は
で与えられ,次式で自然産出量が決定されると仮定する。
ここで
\(A_t=\) \(P_t^{*}\)の変化を決定する項
\(V_t=\) \(P_t^{*}\)に影響を及ぼすランダムなショック
\(B_t=\) \(Y_t^{*}\)の増加を決定する項
\(U_t=\) \(Y_t^{*}\)に影響を及ぼすランダムなショック
一方で,AS曲線とAD曲線を次のように仮定する。
\(V_t\)は\(P_t^{*}\)に影響を与えるという意味で,\(P_t\)に対する恒常的な需要ショックと解釈できる。
\(U_t\)は\(Y_t^{*}\)に影響を与えるという意味で,\(Y_t\)に対する恒常的な需要ショックと解釈できる。
式(120)と(121)の導出#
式(a1)の両辺から式(a3)を引くと次式となる。
2行目は式(120)と同じである。
次に式(a2)の両辺から式(a4)を引くと次式となる。
2行目は式(121)と同じとなっている。
\(Y_t^{*}\)と\(P_t^{*}\)について#
次の仮定を置こう。
1期遅れで自然産出量は\(P_t^{*}\)を減少させる。 自然産出量の増加は生産性の上昇に起因するものであり,それにより物価水準とそのトレンドは減少するというメカニズムを捉えている。
この仮定を使い,式(a3)を次の様に書き換えよう。
\(\Delta P_t^{*}=P_t^{*}-P_{t-1}^{*}\): 物価水準のトレンドの増加率
\(\Delta Y_t^{*}=Y_t^{*}-Y_{t-1}^{*}\): 自然産出量の増加率
この式は,物価水準トレンドの増加率\(\Delta P_t^{*}\)は自然産出量の成長率と比例し,\(V_t\)によりランダムに変動することを示しているの。
次に式(a4)の差分を次の様に計算しよう。
\(\Delta B_t=B_t-B_{t-1}\): 生産性の増加率と解釈する(例えば,
0.02の様な定数にすると毎期2%の成長率となる)\(\Delta U_t=U_t-U_{t-1}\): 恒常的な需要ショックの差分
式(a5)を式(a6)に代入し整理すると次式となる。
式(a7)は自然産出量の成長率を表しており,ランダムなショックにより,変動しながら増加することになる。ショックがない定常状態(\(V_t=U_t=U_{t=1}0\))では
の率で増加することになる。また式(a8)を式(a5)に代入すると次式となる。
自然産出量と同様に,変動しつつ増加することになる。ショックがない定常状態では
の率で増加することになる。
付録B#
残差の自己相関の検定#
Breusch-Godfrey検定を考えよう。
<帰無仮説>
\(H_0\):\(\rho_{p}=0\)
\(H_A\):\(\rho_{p}\ne0\)
from statsmodels.stats.diagnostic import acorr_breusch_godfrey
acorr_breusch_godfrey(res_h, nlags=1)
(5.427205281362893,
0.019825381991796336,
5.50488838698029,
0.020102813691956982)
上から次の値となる。
\(LM\)検定統計量
\(LM\)検定統計量に関する\(p\)値
\(F\)検定統計量
\(F\)検定統計量に関する\(p\)値
5%の有意水準で帰無仮説を棄却できる。即ち,残差の自己相関があるようだ。
次に,Ljung-Box検定もおこなってみよう。
<帰無仮説>
\(H_0\):残差は独立分布
\(H_A\):残差は独立分布ではない
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(res_h.resid, lags=1)
| lb_stat | lb_pvalue | |
|---|---|---|
| 1 | 3.922761 | 0.047637 |
左の値が検定統計量であり,右の値が\(p\)値となる。5%の有意水準で帰無仮説を棄却される。自己相関が疑われる結果である。

