回帰分析#
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import py4macro
import statsmodels.formula.api as smf
# numpy v1の表示を使用
np.set_printoptions(legacy='1.21')
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
はじめに#
この章の目的は２つある。第一に，Pythonを使って回帰分析の方法を紹介する事である。読者には統計学や計量経済学を学び，実際にソフトを使い回帰分析をした経験を持つ人も多く含まれると思う。例えば，無料のRやGretl，そして有料ではあるがStataやEViewsあたりが人気ではないだろうか。Pythonでも回帰分析を簡単におこなうことが可能であり，有名なstatsmodelsとlinearmodelsパッケージを使うと学部の授業で習うことは殆ど全て可能だろう。この章では基本的な回帰分析を考えるのでstatsmodelsだけを取り上げ，その基本的なコードを紹介するが，より多くを知りたい場合は「Pythonで学ぶ入門計量経済学」を参照して欲しい。
この章の第二の目的は，発展会計と成長会計の章で考察した問題を再考することである。その章では，全要素生産性と蓄積生産要素の２つにフォーカスし，それぞれが一人当たりGDPの水準と成長率にどれだけ貢献しているかを考えた。その際，寄与度として分散と共分散を使い計算したが，回帰分析を使うと簡単に計算できる事を示す。
Pythonを使った回帰分析#
発展会計の章で経済間の所得格差の要因を考え，全要素生産性のセクションで全要素生産性と一人当たりGDPの散布図を作成した。そのデータを使い回帰分析のためのコードの書き方を説明する。
データ#
まずデータを作成する。
df2019 = py4macro.data('pwt') \
.query('year == 2019') \
.reset_index(drop=True)
コードの説明
py4macro.data()はDataFrameを返すため，そのメソッドquery()を続けて使っている。またquery()もDataFrameを返すため，そのメソッドreset_index()を続けて使っている。\を使うと改行が可能となる。query('year == 2019')を使って2019年のデータだけを抽出したが，その際に行インデックスが飛び飛びになるので，それを0，1，2….と番号を振り直すためにreset_index()を使っている。引数drop=Trueがないと，元の飛び飛びの行インデックスが新たな列として残るため，それを残さないようにしている。
発展会計の分析で使った同じ変数を作成しよう。
# 資本の所得シャア
a = 1 / 3
# 労働者一人当たりGDP
df2019['gdp_pc'] = df2019['cgdpo'] / df2019['emp']
# 労働者一人当たり資本
df2019['k_pc'] = df2019['ck'] / df2019['emp']
# 蓄積生産要素
df2019['factors'] = df2019['k_pc']**a * ( df2019['avh']*df2019['hc'] )**(1-a)
# 全要素生産性
df2019['tfp'] = df2019['gdp_pc'] / df2019['factors']
# 米国のデータ
us2019 = df2019.query('country == "United States"')
# 労働者一人当たりGDPを標準化（USA=1）
df2019['gdp_pc_relative'] = df2019['gdp_pc'] / us2019['gdp_pc'].to_numpy()
# 全要素生産性の標準化（USA=1）
df2019['tfp_relative'] = df2019['tfp'] / us2019['tfp'].to_numpy()
# 蓄積生産要素の標準化（USA=1）
df2019['factors_relative'] = df2019['factors'] / us2019['factors'].to_numpy()
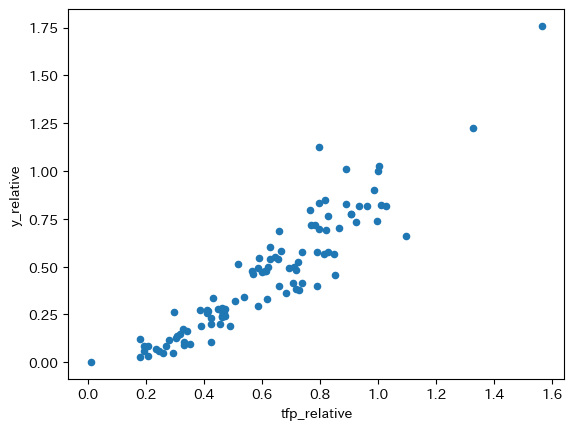
全要素生産性と一人当たりGDPの散布図を作成しよう。
df2019.plot.scatter(x='tfp_relative', y='gdp_pc_relative')
pass
回帰分析#
上の散布図に直線のトレンドの描く場合
となり，iは個々の観測値（即ち，経済）を表す。ここでの目的は，散布図のデータを使い定数項aとスロープ係数bを計算し直線トレンドを描く事である。
式(16)のパラメータbを推計するためにstatsmodelsパッケージを使うが，そのサブパッケージformula.apiの中に含まれるolsを使うことにより、最小二乗法の多くの計算（例えば、検定値など）を自動で行うことが可能である。また推定式を文字列で書くことができるので直感的にコードを書くことが可能となる。より具体的な説明はこのサイトを参照してほしい。
次のステップでコードを書く。
文字列で推定式を書く。
smfに含まれるols()関数を使って推定の準備を行う。メソッド
.fit()を使って自動計算を行う。結果の属性やメソッドを使い推定値を表示する。
＜ステップ１＞ 推定式の設定
回帰式は次のような形で文字列を使って指定する。
'被説明変数 ~ 定数項以外の説明変数'
定数項は自動的に挿入される。また定数項以外の説明変数が複数がる場合は、+でつなげるが，今回は単回帰分析となるので説明変数は１つとなる。また回帰式の中で使う変数名は，データが含まれるDataFrameの列ラベルを使う。
'gdp_pc_relative ~ tfp_relative'
以下ではこの回帰式を変数formulaに割り当てているが，変数は分かりやすいものであれば好きなものを使えば良い。
formula = 'gdp_pc_relative ~ tfp_relative'
＜ステップ２＞ 自動計算の準備
smfのols()関数を使って自動計算の準備として計算の対象となるもの（インスタンスと呼ばれるオブジェクト）を生成する。次のコードでは変数modelに割り当てる。
model = smf.ols(formula, data=df2019)
ols()の第１引数は上で定義した文字列の回帰式であり、第２引数dataは使用するデータを指定する。
＜ステップ３＞ 自動計算
modelのメソッド.fit()を使って自動計算し，計算した結果を変数resultに割り当てる。
result = model.fit()
ここでステップ２と３を連続で次のように書いても構わない。
result = ols(formula, data=df).fit()
＜ステップ４＞ 結果の表示
resultには様々な属性が用意されているが、メソッド.summary()を使うと基本的な推定結果を表示することができる。（関数print()を使っているが使わなくても同じ情報が表示される。）
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: gdp_pc_relative R-squared: 0.851
Model: OLS Adj. R-squared: 0.848
Method: Least Squares F-statistic: 336.7
Date: Tue, 10 Dec 2024 Prob (F-statistic): 4.64e-26
Time: 23:25:46 Log-Likelihood: 49.767
No. Observations: 61 AIC: -95.53
Df Residuals: 59 BIC: -91.31
Df Model: 1
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept -0.2821 0.049 -5.812 0.000 -0.379 -0.185
tfp_relative 1.2005 0.065 18.349 0.000 1.070 1.331
==============================================================================
Omnibus: 12.607 Durbin-Watson: 1.985
Prob(Omnibus): 0.002 Jarque-Bera (JB): 18.207
Skew: 0.730 Prob(JB): 0.000111
Kurtosis: 5.243 Cond. No. 7.14
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
表は3つのセクションから構成されている。
上段にはOLS推定の基本的な情報が表示されている。
左側
Dep. Variable：被説明変数Model：モデルMethod：手法Data：日にちTime：時間No. Observation：標本の大きさDf Residuals：残差の自由度Df Model：モデルの自由度（定数項以外の説明変数の数）Covariance Type：共分散のタイプ
右側
R-squared：決定係数adj. R-squared：自由度調整済み決定係数F-statistic：\(F\)統計量Prob (F-statistic)：\(F\)値Log-Likelihood：対数尤度AIC：赤池情報量規準BIC：ベイズ情報量規準
中段には主な推定結果が表示される。
列ラベル
coef：係数std err：標準誤差t：\(t\)値P>|t|：\(p\)値[0.025,0.975]：信頼区間（5%)
行ラベル
Intercept：定数項tfp_relative：説明変数（選択する変数によって変わる）
下段には様々な検定などに関する数値が並んでいる。
左側
Omnibus：オムニバス検定統計量（帰無仮説：残差は正規分布に従う）Prob(Omnibus)：オムニバス検定\(p\)値Skew：残差の歪度（正規分布であれば0）Kurtosis：残差の尖度（正規分布であれば3）
右側
Durbin-Watson：ダービン・ワトソン統計量（残差の自己相関の検定）Jarque-Bera (JB)：ジャーク・ベラ検定統計量（帰無仮説：残差は正規分布に従う）Prob(JB)：ジャーク・ベラ検定\(p\)値Cond. No.：条件指数（Condition Index）の最大値（多重共線性を確認するための指標だが，変数が標準化されて計算していないため変数の値の大きさに依存することになるり，使い難い指標となっている。重回帰分析においての多重共線性の確認についてはここで説明する手法を使うことを勧める。）
必要な部分だけを表示する場合は，次のコードを使うと良いだろう。
result.summary().tables[0]
result.summary().tables[1]
result.summary().tables[2]
係数の推定値に関する中段の表を表示してみる。
print(result.summary().tables[1])
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept -0.2821 0.049 -5.812 0.000 -0.379 -0.185
tfp_relative 1.2005 0.065 18.349 0.000 1.070 1.331
================================================================================
Note
statsmodels 13.0では.summary()に引数slim（デフォルトはFalse）が追加されており，.tablesを使わずに次のコードで簡略化された表を表示できる。
result.summary(slim=True)
結果の解釈を試みてみよう。
定数項の推定値のp値は小さく、通常の有意水準では「定数項の値はゼロ」の帰無仮説を棄却できる。一方で，一人当たりGDPは正の値を取るが，定数項はマイナスの値となっている。ここでは非線形の関係が示唆されるので，練習問題で再考する。
tfp_relativeのパラメータの推定値は正の値であり，統計的優位性も高い。推定値を解釈するために，相対的全要素生産性であるtfp_relativeが0.01上昇したとしよう（例えば，0.5から0.51）。相対的一人当たりGDPgdp_pc_relativeは平均で1.2225x0.01=0.012225増加する事になる。即ち，全要素生産性の１単位の上昇は一人当たりGDPの１単位以上の増加につながっている。
resultは推定結果に関する情報が詰まったオブジェクトである。何が備わっているかpy4macroモジュールに含まれるsee()関数を使って調べてみよう。
py4macro.see(result)
.HC0_se .HC1_se .HC2_se .HC3_se
.aic .bic .bse .centered_tss
.compare_f_test .compare_lm_test .compare_lr_test .condition_number
.conf_int .conf_int_el .cov_HC0 .cov_HC1
.cov_HC2 .cov_HC3 .cov_kwds .cov_params
.cov_type .df_model .df_resid .diagn
.eigenvals .el_test .ess .f_pvalue
.f_test .fittedvalues .fvalue .get_influence
.get_prediction .get_robustcov_results .info_criteria .initialize
.k_constant .llf .load .model
.mse_model .mse_resid .mse_total .nobs
.normalized_cov_params .outlier_test .params .predict
.pvalues .remove_data .resid .resid_pearson
.rsquared .rsquared_adj .save .scale
.ssr .summary .summary2 .t_test
.t_test_pairwise .tvalues .uncentered_tss .use_t
.wald_test .wald_test_terms .wresid
推定結果の表を表示するメソッド.summary()が含まれていることが分かる。その他様々なものが含まれているが，詳細はこのサイト（英語）を参考にして欲しい。ここでは代表的なものだけを紹介する。
まず係数の推定値はresultの属性paramsでアクセスできる。
result.params
Intercept -0.282074
tfp_relative 1.200503
dtype: float64
result.paramsのタイプを調べてみよう。
type(result.params)
pandas.core.series.Series
PandasのSeriesとして返されていることが分かる。従って，定数項は.iloc[]とインデックス番号を使ってresult.params[0]，スロープ係数はresult.params[1]で抽出できる。
ahat = result.params.iloc[0]
bhat = result.params.iloc[1]
ahat, bhat
(-0.282074443950234, 1.2005026319194922)
もしくは，ラベルを使うこともできる。その場合は，[]もしくは.loc[]を使うと良い。
ahat = result.params['Intercept']
bhat = result.params['tfp_relative']
# これでも同じ結果となる
# ahat = result.params.loc['Intercept']
# bhat = result.params.loc['tfp_relative']
ahat, bhat
(-0.282074443950234, 1.2005026319194922)
この方法を使い，tfp_relativeがxの場合のgdp_pc_relativeを計算する関数は作ってみよう。
def calculate_gdp_pc_relative(x):
gdp = result.params.iloc[0]+result.params.iloc[1]*x
print(f'相対全要素生産性が{x}の場合の相対的一人当たりGDPは約{gdp:.3f}です。')
xが0.8の場合を考えよう。
calculate_gdp_pc_relative(0.8)
相対全要素生産性が0.8の場合の相対的一人当たりGDPは約0.678です。
Note
予測値だけであれば，次のコードでも同じ結果を表示できる。
result.predict({'tfp_relative':0.8})
ここで.predict()は予測値を得るメソッド。引数を入れずに使うと，次に説明する属性.fittedvaluesと同じ値を返す。
次に、標本の散布図に回帰直線を重ねて表示してみる。まずresultの属性.fittedvaluesを使い非説明変数の予測値を抽出することができるので、df2019にfittedのラベルを使って新たな列として追加する。
df2019['OLS fitted'] = result.fittedvalues
図を重ねて表示する。
ax_ = df2019.plot.scatter(x='tfp_relative', y='gdp_pc_relative')
df2019.sort_values('OLS fitted').plot(x='tfp_relative',
y='OLS fitted',
color='r', ax=ax_)
pass
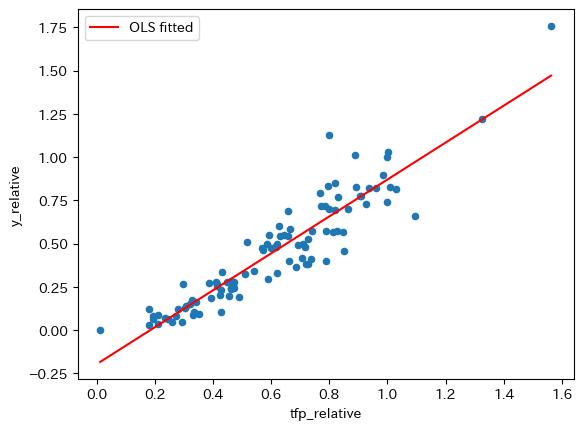
コードの説明
２行目のsort_values()は引数の'OLS fitted'を基準に昇順に並べ替える。これを指定しないと直線が綺麗に表示されない。
Note
gdp_pc_relativeの予測値は，属性.fittedvaluesもしくはメソッド.predict()で取得できるが，次のコードでも同じ結果となる。
df2019['fitted'] = ahat + bhat * df2019.loc[:,'tfp_relative']
回帰分析による発展会計#
説明#
発展会計の式(5)では，米国の一人当たりGDPを基準として経済\(i\)の一人当たりGDPを次式で表した。
ここで，
\(r_i^y\)：一人当たりGDP（対数; 米国＝１）
\(r_i^{\text{tfp}}\)：全要素生産性（対数; 米国＝１）
\(r_i^{\text{factors}}\)：蓄積生産要素（対数; 米国＝１）
また，それぞれの貢献度を次式で数量化した。
この章では回帰分析を使って\(\beta_{\text{tfp}}\)と\(\beta_{\text{factors}}\)計算することができることを示す。そのために，まず次の関係が成立することを思い出そう。
これらを使うと(18)は次のように書き換えることができる。
蓄積生産要素の寄与度についても同様に次式で与えられる。
この結果が回帰分析とどのような関係にあるかを確認するために，次の単回帰式を考えよう。
最小二乗法を使い推定すると，スロープ係数の推定値は次式で与えられることになる。
式(22)と２つの式(20)と(21)から，次の回帰式を最小二乗法で推定すると\(\beta_{\text{tfp}}\)と\(\beta_{\text{factors}}\)を計算できることが分かる。
以下ではstatsmodelsを使って実際に計算してみよう。
最小二乗法による計算#
df2019にある変数を使って，計算に使う変数を作成しよう。
# 労働者一人当たりGDP（USA=1）の対数化
df2019['gdp_pc_relative_log'] = np.log( df2019['gdp_pc_relative'] )
# 全要素生産性（USA=1）の対数化
df2019['tfp_relative_log'] = np.log( df2019['tfp_relative'] )
# 蓄積生産要素（USA=1）の対数化
df2019['factors_relative_log'] = np.log( df2019['factors_relative'] )
次に推定式を定義する。
formula_tfp = 'tfp_relative_log ~ gdp_pc_relative_log'
formula_factors = 'factors_relative_log ~ gdp_pc_relative_log'
自動計算のための準備をし，実際に計算した結果を変数に割り当てる。
result_tfp = smf.ols(formula_tfp, data=df2019).fit()
result_factors = smf.ols(formula_factors, data=df2019).fit()
パラメータの値を表示してみよう。
print(f'全要素生産性の寄与度：{result_tfp.params.iloc[1]}\n'
f'蓄積生産要素の寄与度：{result_factors.params.iloc[1]}')
全要素生産性の寄与度：0.5467723234514837
蓄積生産要素の寄与度：0.45322767654851603
コードの説明
fは以前説明したf-stringを使って{}に値を代入している。()は複数行にしても構わない。''で囲んだ文字列を複数行にする場合は，それぞれの行で閉じる必要がある。\nは改行という意味。
全要素生産性と蓄積生産要素の寄与度で計算した値と同じになることが確認できる。